The radius of a sphere is increasing at a rate of 2 meters per second. At what rate is the volume increasing when the radius is equal to 4 meters?
This type of problem is known as a "related rate" problem. In this sort of problem, we know the rate of change of one variable (in this case, the radius) and need to find the rate of change of another variable (in this case, the volume), at a certain point in time (in this case, when r = 4). The reason why such a problem can be solved is that the variables themselves have a certain relation between them that can be used to find the relation between the known rate of change and the unknown rate of change.
Related rate problems can be solved through the following steps:
Step one: Separate "general" and "particular" information.
General information is information contained in the problem that is true at all times.
Particular information is information that is true only at the particular instant that the
problem is asking about.
For example, in this problem, the general information is that the radius is growing at a rate of 2 meters per second. Thus, if we let the radius of the sphere be represented by r, we can say that r'(t)=2 m/s.
The particular information is that at the moment of interest, r(t) = 4.
It is important to separate out these two types of information because information about the particular case must be set aside and must not be used until the very last step of solving the problem. One mistake that students frequently make is to use the particular information too early. This invariably leads to incorrect answers.
Step two: Draw a sketch of the situation using the general information only.
This often helps to illuminate the relationship between the variables.
In this case, the general information leads to the following sketch:
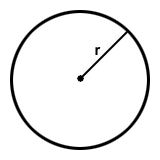
Although we know the rate of change of r, we cannot depict a rate in the sketch.
Note here that it would be a mistake to write "r = 4" in the sketch, since this is only true at one particular instant.
Step three: Identify the known rate and the desired rate
In this case, we know 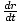 , and we want to find
, and we want to find 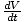 , the rate of
change of the volume.
, the rate of
change of the volume.
Step four: Use geometry or trigonometry to relate the variable with the known
rate of change to the variable with the unknown rate of change.
The appropriate relation will often involve one of the following:
- Spheres: Radius vs. Surface area (4Πr2)vs. Volume (
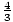 Πr3)
Πr3)
- Circles: Radius vs. Area (Πr2) vs. Circumference (2Πr)
- Cylinders: Radius and Height vs. Volume (Πr2h)
- Cones: Radius and Height vs. Volume (
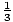 Πr2h) Also see similar
triangles below.
Πr2h) Also see similar
triangles below.
- Right Triangles: Pythagorean Theorem (a2 + b2 = c2)
- Similar Triangles:
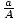 =
= 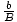 =
= 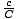
- Angles: Problems with angles will typically involve a trigonometric relation. Recall the
"SOHCAHTOA" relations (sin =
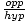 , cos =
, cos = 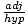 , and
tan =
, and
tan = 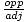 )
)
-
In this case, the appropriate relation is
V = 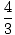 Πr3
Πr3
Recall that both V and r are variables with change with time. Therefore, it is best to write the relation in a way that indicates this fact:V(t) = 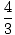 Π
Π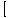 r(t)
r(t)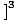
Step Five: Differentiate both sides of the equation with respect to time Now that we have found a relationship between the variables, we must differentiate both sides of the equation to find a relationship between their rates of change (i.e., their derivatives). It is crucial to remember to use the chain rule here, since we are taking derivatives with respect to t:
V(t) = 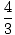 Π
Π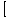 r(t)
r(t)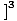
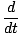
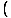 V(t)
V(t)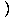 =
= 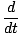
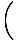
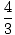 Π
Π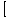 r(t)
r(t)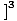
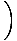
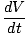 = 4Π
= 4Π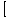 r(t)
r(t)

Step 6: Plug in the particular information to solve for the desired rate. Now, we can finally use the particular fact that r = 4 to solve for the unknown rate:
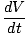 = 4Π
= 4Π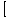 r(t)
r(t)

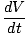 = 4Π
= 4Π 4
4 2
2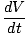 = 128Π
= 128Π
So, when the radius is 4 meters long, the volume is increasing at a rate of 128Π cubic meters per second.


 payment page
payment page



