Definite Integral
Terms
Antiderivative
-
An antiderivative of a function
f (x)
is a function
F(x)
such that
F'(x) = f (x)
.
Definite Integral
-
The limit approached by the
n
th upper and lower Riemann sums as
n→∞
.
Integrable
-
The property that the definite integral of a function exists; that is, the upper and lower
Riemann sums converge to the same value as the size of the approximating rectangles shrinks to
zero.
Riemann Sum
-
The sum of areas of rectangles approximating the area under the graph of a function; examples
include the upper and lower Riemann sums.
Fundamental Theorem of Calculus
-
The relationship between differentiation and integration:
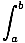F'(x)dx
|
= F(b) - F(a) | ||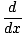
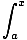f (t)dt
|
= f (x) |
Lower Riemann Sum
-
An approximation to the area below the graph of a function, equal to the total area of a
number of thin rectangles inscribed in the region below the graph.
Upper Riemann Sum
-
An approximation to the area below the graph of a function, equal to the total area of a
number of thin rectangles containing the region below the graph.
Telescoping Limits
-
The following property of the definite integral:
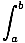f (x)dx + 
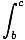f (x)dx = 
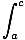f (x)dx
|
