payment page
-
Acute Angle
An angle whose measure is less than 90 degrees.
-
Adjacent Angle
Angles that share a vertex, one side, and no interior points.
-
Alternate Exterior Angles
Angles created when a transversal intersects with two lines. Alternate exterior angles lie on opposite sides of the transversal, and on the exterior of the space between the two lines.
-
Alternate Interior Angles
Angles created when a transversal intersects with two lines. Alternate interior angles lie on opposite sides of the transversal, and on the interior of the space between the two lines. That is, they lie between the two lines that intersect with the transversal.
-
Angle
A geometric figure consisting of the union of two rays that share a common endpoint.
-
Angle Bisector
A ray that shares a common vertex with an angle, lies within the interior of that angle, and creates two new angles of equal measure.
-
Angle Trisector
A ray, one of a pair, that shares a common vertex with an angle, lies within the interior of that angle, and creates, with its partner, three new angles of equal measure. Angle trisectors come in pairs.
-
Complementary Angles
A pair of angles whose measures sum to 90 degrees. Each angle in the pair is the other's complement.
-
Congruent
Of the same size. Angles can be congruent to other angles and segments can be congruent to other segments.
-
Corresponding Angles
A pair of angles created when a transversal intersects with two lines. Each angle in the pair is on the same side of the transversal, but one is in the exterior of the space created between the lines, and one lies on the interior, between the lines.
-
Degree
A unit of measure for the size of an angle. One full rotation is equal to 360 degrees. A right angle is 90 degrees. One degree equals
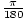radians.
-
Exterior Angle
The larger part of an angle. Were one of the rays of an angle to be rotated until it met the other ray, an exterior angle is spanned by the greater rotation of the two possible rotations. The measure of an exterior angle is always greater than 180 degrees and is always 360 degrees minus the measure of the interior angle that accompanies it. Together, an interior and exterior angle span the entire plane.
-
Interior Angle
The smaller part of an angle, spanned by the space between the rays that form an angle. Its measure is always less than 180 degrees, and is equal to 360 degrees minus the measure of the exterior angle.
-
Midpoint
The point on a segment that lies exactly halfway from each end of the segment. The distance from the endpoint of a segment to its midpoint is half the length of the whole segment.
-
Oblique
Not perpendicular.
-
Obtuse Angle
An angle whose measure is greater than 90 degrees.
-
Parallel Lines
Lines that never intersect.
-
Parallel Postulate
A postulate which states that given a point not located on a line, exactly one line passes through the point that is parallel to original line.
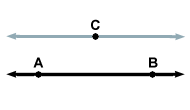
Figure %: The parallel postulate -
Perpendicular
At a 90 degree angle. A geometric figure (line, segment, plane, etc.) is always perpendicular to another figure.
-
Perpendicular Bisector
A line or segment that is perpendicular to a segment and contains the midpoint of that segment.
-
Radian
A unit for measuring the size of an angle. One full rotation is equal to 2Π radians. One radian is equal to
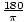degrees.
-
Ray
A portion of a line with a fixed endpoint on one end that extends without bound in the other direction.
-
Right Angle
A 90 degree angle. It is the angle formed when perpendicular lines or segments intersect.
-
Segment Bisector
A line or segment that contains the midpoint of a segment.
-
Straight Angle
A 180 degree angle. Formed by two rays that share a common vertex and point in opposite directions.
-
Supplementary Angles
A pair of angles whose measures sum to 180 degrees. Each angle in the pair is the other's supplement.
-
Transversal
A line that intersects with two other lines.
-
Vertex
The common endpoint of two rays at which an angle is formed.
-
Vertical Angles
Pairs of angles formed where two lines intersect. These angles are formed by rays pointing in opposite directions, and they are congruent. Vertical angles come in pairs.
-
Zero Angle
A zero degree angle. It is formed by two rays that share a vertex and point in the same direction.
