-
Argument
The angle created by the positive real axis and the segment connecting the origin to the plot of a complex number in the complex plane.
-
Complex Conjugate
The complex conjugate of a given complex number a + bı is a - bı.
-
Complex Number
The set of all numbers of the form a + bı, where a and b are real numbers. The real numbers are all complex numbers.
-
Complex Plane
A plane with two perpendicular axes, the real axis and the imaginary axis, on which a complex number a + bı is plotted at the coordinate (a, b). It is customary for the real axis to coincide with the x-axis of the rectangular coordinate system, and for the imaginary axis to coincide with the y-axis of the rectangular coordinate system.
-
Imaginary Axis
The axis in the complex plane that customarily coincides with the y-axis of the rectangular coordinate system, and on which the imaginary part bı of the complex number a + bı is plotted.
-
Imaginary Number
A number that can be expressed in the form bı, where b is a real number.
-
Imaginary Part
The bı term in every complex number a + bı.
-
Imaginary Unit
The imaginary unit is ı. ı =
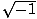 .
.
-
Modulus
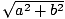 for a complex number a + bı. In the complex
plane, it is the distance between the plot of a complex number and the
origin.
for a complex number a + bı. In the complex
plane, it is the distance between the plot of a complex number and the
origin.
-
Polar Form of a Complex Number
The polar form of a complex number z = a + bı is this: z = r(cos(θ) + ısin(θ)), where r = | z| and θ is the argument of z.
-
Real Axis
The axis in the complex plane that typically coincides with the x-axis of the rectangular coordinate system, and on which the real part a of a complex numbers a + bı is plotted.
-
Real Part
In a complex number a + bı, a.
-
Standard Form
For a complex number, a + bı.
Terms
Formulae
| De Moivre's Theorem | Let z = r(cos(θ) + ısin(θ).Thenzn = [r(cos(θ) + ısin(θ)]n = rn(cos(nθ) + ısin(nθ), where n is any positive integer. |
| Roots of a Complex Number |
A complex number z = r(cos(θ) + ısin(θ) has exactly nnth roots given by the equation 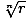 [cos( [cos(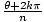 ) + ısin( ) + ısin(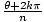 )], where n is a positive integer, and k = 0, 1, 2,..., n - 2, n - 1. )], where n is a positive integer, and k = 0, 1, 2,..., n - 2, n - 1.
|


 payment page
payment page



