payment page
-
Continuity
A function is continuous at a point if the three following conditions are met: 1) f (a) is defined. 2)
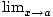f (x) exists. 3) 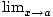f (x) = f (a). A conceptual way to describe continuity is this: A function is
continuous if its graph can be traced with a pen without lifting the pen from
the page.
-
Infinite Discontinuity
A category of discontinuity in which a vertical asymptote exists at x = a and f (a) is undefined.
-
Jump Discontinuity
A category of discontinuity in which
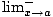f (x)≠
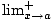f (x), but both of these limits exist and are finite.
-
Limit
The value A to which a function f (x) gets arbitrarily close as the value of the independent variable x gets arbitrarily close to a given value a. Such a limit is symbolized this way: limxâÜ’af (x) = A.
-
One-Sided Limit
A limit based entirely on the values of a function taken at an x-value slightly greater than or less than a given value. Whereas a two-sided limit
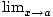f (x) takes into account the values of x near a which are
both greater than and less than a, a one-sided limit from the left 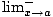f (x) or from the right 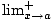f (x) takes into account only
values of x less than a, or greater than a, respectively.
-
Point Discontinuity
A category of discontinuity in which a function has a well-defined two-sided limit at x = a, but either f (x) is not defined at a or its value at a is not equal to this limit.
