Using vector calculus, we can generate some properties of any magnetic field, independent of the particular source of the field.
Line Integrals of Magnetic Fields
Recall that while studying electric fields we
established that the surface integral through any closed surface in the field
was equal to 4Π times the total charge enclosed by the surface. We wish to
develop a similar property for magnetic fields. For magnetic fields, however,
we do not use a closed surface, but a closed loop. Consider a closed circular
loop of radius r about a straight wire carrying a current I, as shown below.
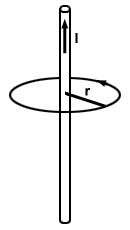
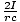 . In addition, the total length of the path is simply the
circumference of the circle: l = 2Πr. Thus, because the field is constant on
the path, the line integral is simply:
. In addition, the total length of the path is simply the
circumference of the circle: l = 2Πr. Thus, because the field is constant on
the path, the line integral is simply:
lineintegral
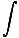 B·ds = Bl = B·ds = Bl = 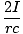 (2Πr) = (2Πr) = 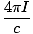 |
This equation, called Ampere's Law, is quite convenient. We have generated an equation for the line integral of the magnetic field, independent of the position relative to the source. In fact, this equation is valid for any closed loop around the wire, not just a circular one (see problems).
@@Equation @@ can be generalized for any number of wires carrying any number of currents in any direction. We won't go through the derivation, but will simply state the general equation.
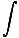 B·ds = B·ds = 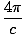 × total current enclosed by path × total current enclosed by path |
Note that the path need not be circular or perpendicular to the wires. The figure below shows a configuration of a closed path around a number of wires:
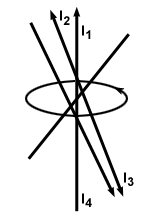
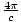 (I1 + I2 - I3 - I4). Notice that the two wires pointing downwards
are subtracted, since their field points in the opposite direction from the
curve.
(I1 + I2 - I3 - I4). Notice that the two wires pointing downwards
are subtracted, since their field points in the opposite direction from the
curve.
This equation, similar to the surface integral equation for electric fields, is powerful and allows us to greatly simplify many physical situations.
The Curl of a Magnetic Field
From this equation, we can generate an expression for the curl of a magnetic field. Stokes' Theorem states that:
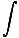 B·ds =
B·ds = 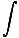 curl B·da
curl B·da
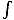 B·ds =
B·ds = 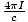 . Thus:
. Thus:
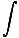 curl B·da =
curl B·da = 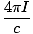
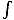 J·da. Substituting this into our
equation, we find that
J·da. Substituting this into our
equation, we find that
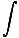 curl B·da =
curl B·da = 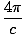
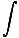 J·da
J·da
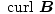 = = 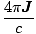 |
Thus the curl of a magnetic field at any point is equal to the current density at that point. This is the simplest statement relating the magnetic field and moving charges. It is mathematically equivalent to the line integral equation we developed before, but is easier to work with in a theoretical sense.
The Divergence of the Magnetic Field
Recall that the divergence of the electric field was equal to the total charge density at a given point. We have already examined qualitatively that there is no such thing as magnetic charge. All magnetic fields are, in essence, created by moving charges, not by static ones. Thus, because there are no magnetic charges, there is no divergence in a magnetic field:
 = 0 = 0 |
This fact remains true for any point in any magnetic field. Our expressions for divergence and curl of a magnetic field are sufficient to describe uniquely any magnetic field from the current density in the field. The equations for divergence and curl are extremely powerful; taken together with the equations for the divergence and curl for the electric field, they are said to encompass mathematically the entire study of electricity and magnetism.


 payment page
payment page



