Problem :
A uniform magnetic field in the positive y direction acts on a positively charged particle moving in the positive x direction. In what direction does the force act on particle?
To solve this problem we simply use the right hand rule. First we construct a
three dimensional axis, as shown below. Then we point our thumb in the positive
x direction, our index finger in the positive y direction, and we find that our
middle finger points in the positive z direction, implying that this is exactly
the direction of the force on the particle.

Problem :
Two vectors, v1 and v2, each with magnitude of 10, act in the x-y plane,
at an angle of 30o, as shown below. What is the magnitude and
direction of the cross product v1×v2?
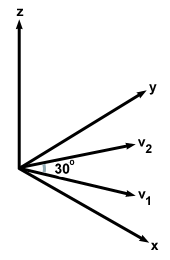
Finding the magnitude of the cross product is easy: it is simply v1v2sinθ = (10)(10)(.5) = 50. The direction of the cross product, however, takes a little thought. Since we are computing v1×v2, think of v1 as a velocity vector, and v2 as a magnetic field vector. Using the right hand rule, then, we find that the cross product of the two points in the positive z direction. Notice from this problem that cross products are not communative: the direction of v1×v2 is the opposite of that of v2×v1. This problem should help with the complicated directions of fields, velocities, and forces.
Problem :
A uniform electric field of 10 dynes/esu acts in the positive x direction, while a uniform magnetic field of 20 gauss acts in the positive y direction. A particle of charge q and velocity of .5c moves in the positive z direction. What is the net force on the particle?
To solve the problem we use the equation:
 = q = q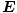 + + 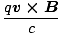 |
So we must find the vector sum of the electric force and the magnetic force. The electric force is easy: it is simply qE = 10q in the positive x direction. To find the magnetic force, we must use the right hand rule (again), and find that the force on the particle must act in the negative x direction. Thus we must now find the magnitude of the force. Since v and B are perpendicular, we do not need to compute a cross product, and the equation simplifies to FB =
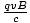 =
= 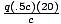 = 10q. Since this force acts in the
negative x direction, it exactly cancels the electric force on the particle.
Thus, even though both an electric field and a magnetic field act on the
particle, it experiences no net force.
= 10q. Since this force acts in the
negative x direction, it exactly cancels the electric force on the particle.
Thus, even though both an electric field and a magnetic field act on the
particle, it experiences no net force.
Problem :
A charged particle moving perpendicular to a uniform magnetic field always experiences a net force perpendicular to its motion, similar to the kind of force experienced by particles moving in uniform circular motion. The magnetic field can actually cause the particle to move in a complete circle. Express the radius of this circle in terms of the charge, mass and velocity of the particle, and the magnitude of the magnetic field.
In this case the magnetic field produces the centripetal
force required to move the
particle in uniform circular motion. We know that, since v is perpendicular to
B, the magnitude of the magnetic force is simply FB = 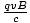 . We also
know that any centripetal force has magnitude Fc =
. We also
know that any centripetal force has magnitude Fc =  . Since the
magnetic force is the only one acting in this situation, we may relate the two
quantities:
. Since the
magnetic force is the only one acting in this situation, we may relate the two
quantities:
| Fc | = | FB | |
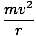 | = | 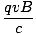 | |
| mv2c | = | qvBr | |
| r | = | 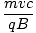 |
Analyzing our answer we see that stronger fields cause particles to move in smaller circles.


 payment page
payment page



