Problem :
Two wires run parallel to each other, each with a current of 109 esu/sec. If each wire is 100 cm long, and the two wires are separated by a distance of 1 cm, what is the force between the wires?
This is the simplest case of magnetic interaction between currents, and we simply plug in values to our equation:
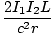 =
=  = .222
dynes
= .222
dynes
Problem :
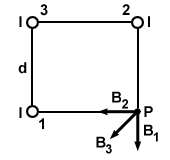
Three wires, each with a current of i, run parallel and go through three corners
of a square with sides of length d, as shown below. What is the magnitude and
direction of the magnetic field at the other corner?

To find the net magnetic field, we must simply find the vector sum of the contributions of each wire. The wires on the corners contribute a magnetic field of the same magnitude but are perpendicular to each other. The magnitude of each is:
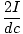
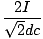
| Bx | = | - B2 - B3sin 45o = - 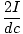 - - 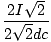 = - = -  | |
| By | = | - B1 - b3sin 45o = - 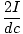 - - 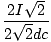 = - = -  |
Notice from the symmetry of the problem that the x and y components have the same magnitude, as expected. Also from symmetry we can tell that the net force will act in the same direction as the field from B3, down and to the left. Its magnitude comes from the vector sum of the two components:
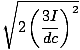 = 3
= 3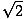
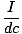
Problem :
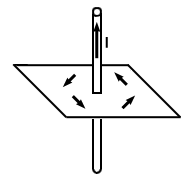
Compass needles are placed at four points surrounding a current carrying wire,
as shown below. In what direction does each needle point?
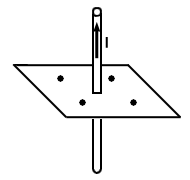
Compasses in the presence of a magnetic field will always point in the direction
of the field lines. Using the right hand rule we see that the field lines flow
counterclockwise, as seen from above. Thus the compasses will point as such:
Problem :
What is the force felt by a particle with charge q travelling parallel to a wire with current I, if they are separated by a distance r?
We have derived the force felt by another wire, but have not derived it for a
single particle. Clearly the force will be attractive, as the single charge can
be seen as a "mini current" running parallel to the wire. We know that
B = 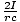 , and that F =
, and that F = 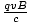 , since the field and the velocity
of the particle are perpendicular. Thus we simply plug in our expression for B:
, since the field and the velocity
of the particle are perpendicular. Thus we simply plug in our expression for B:
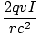
Problem :
Two parallel wires, both with a current I and length l, are separated by a
distance r. A spring with constant k is attached to one of the wires, as shown
below. The strength of the magnetic field can be measured by the distance the
spring is stretched due to the attraction between the two wires. Assuming that
the displacement is small enough that at any time the distance between the two
wires can be approximated by r, generate an expression for the displacement of
the wire attached to the spring in terms of I, r, l and k.
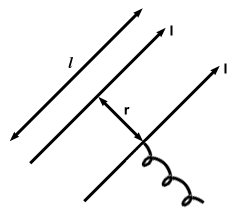
The spring will reach its maximum displacement when the force exerted by one wire on the other is in equilibrium with the restoring force of the spring. At its maximum displacement, x, the distance between the two wires is approximated by r. Thus the force on one wire by the other at this point is given by:
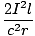
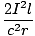 | = | kx | |
| x | = | 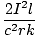 |
Although we did use an approximation to find the answer, this method is a useful way of determining the strength of the magnetic force between two wires.


 payment page
payment page



