-
Principle of superposition
When any two waves occupy the same point or region in space, the resulting disturbance of the medium is the sum of the disturbances of the individual waves (in other words, just add the amplitudes, paying attention to the sign). This is the same as saying that the wave equation is linear: if μ1 and μ2 are solutions, then aμ1 + bμ2 are also solutions, for some constants a and b. One consequence of this is that two or more waves can pass through each other with each being unaffected by the other.
-
Fermat's principle
The path taken by a light ray will be the one that minimizes the time taken in passing between any two points. This is equivalent to saying that the duration of the path taken by light is stationary with respect to small variations in the path.
-
Scattering
This occurs when light is incident on an atom. The oscillating electric and magnetic fields of the light wave cause the electrons in the atom to vibrate at the same frequency as the incident wave, causing a re-radiation of light in all directions (a spherical wave) about the atom. The light is said to be scattered by the atom. Such scattering is always elastic.
-
Longitudinal wave
An oscillation in which the displacement of the particles of the medium about their equilibrium position is in the direction parallel to the direction of propagation. Longitudinal waves exhibit many of the opposite behaviors to transverse waves (for example, they speed up in denser media). Sound is a longitudinal wave.
-
Transverse wave
An oscillation in which the displacement of the particles of the medium about their equilibrium position is in a direction perpendicular to the direction of propagation. Light is a transverse wave.
-
Harmonic
Waves that take on the shape determined by the harmonic functions, sine and cosine. They are also called sinusoidal waves or simple harmonic waves. Not only are these functions simple to deal with, but Fourier analysis tells us that any wave can by synthesized by the superposition of harmonic waves.
-
Phase
In a harmonic function, the phase the argument of the sine or cosine function. In general it is given by: ψ(x, t) = (kx - σt + ε), where ε is called the initial phase. The phase determines whether the wave is at a peak or trough or somewhere in between at a particular point in space and time.
-
Amplitude
The maximum disturbance, or the maximum displacement of the particles of the medium from their equilibrium position. This is given by the constant term preceding the sine or cosine in a harmonic wave.
-
Wavelength
The wavelength of a wave is denoted λ and is the distance in space from one peak to any adjacent peak, one trough to any adjacent trough, or indeed from any one point to a similar point on an adjacent cycle. In other words, it is the number of units of length per complete wave cycle.
-
Wavenumber
Denoted k, the wavenumber is the constant that appears in the expression for the phase (usually the coefficient of x). It is defined as k = 2Π/λ, and as such as units of inverse length.
-
Frequency
Denoted ν, the frequency is the number of complete wave cycles which pass a given point in space in one unit of time (one second). It is the inverse of the period of the wave (and has units of inverse time, or 1 Hertz = 1 second-1), and is given by ν = v/λ.
-
Angular frequency
Denoted σ, the angular frequency is the number of radians of a harmonic wave which pass a given point per unit time (second). One complete wave cycle has 2Π radians, so the angular frequency is given by σ = 2Πν. It also has units of inverse time (or radians per second, but radians are not proper units and are dimensionless).
-
Period
The amount of time T taken for a complete wave cycle to pass a particular point. In other words, the number of units of time per wave. It has units of time and is the inverse of the frequency.
-
Phase velocity
Is the speed of propagation of the condition of constant phase. What this means is that the phase velocity is the speed at which you would have to be traveling alongside the wave in order to observe to change in the phase of the wave next to you. In other words, it is the speed of propagation of a particular crest or trough. It is not hard to deduce from the wave equation that v = σ/k = λν.
-
Photon
A quanta of light. Photons are particles that have no mass or charge and travel only at speed c, regardless of medium or reference frame. They have an energy given by E = hν where ν is the frequency of the light to which they correspond, and h = 6.626×10-34 J.s (Planck's constant). We can account for the behavior of light by considering it as consisting of a very large number of photons. In this regime the electromagnetic field appears continuous and the granularity of the light beam is negligible.
-
Poynting vector
Named after John Henry Poynting (1852-1914), this is given by:
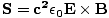
This is the unit power per area crossing a surface with normal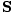 . The direction of
. The direction of 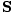 is
parallel to the direction of the propagation of the light ray.
is
parallel to the direction of the propagation of the light ray.
-
Spherical wave
The linear wave described in Waves is not the only solution to the wave equation. In three-dimensions plane and spherical waves can also exist. In spherical waves, the disturbance of the medium is a function of r, isotropic in all directions (think of two-dimensional circular waves generated by dropping a stone into a pond). The wavefronts are spheres. The symmetry of spherical waves makes them very important when optics is treated in three-dimensions.
-
Absorb
When light is incident on an atom, if its frequency corresponds to a possible quantum jump between energy levels for the electrons in that atom, it may be absorbed, and the atom excited into a higher energy state. Usually this excitation energy is very rapidly transferred, via collisions into thermal motion (for this reason it is sometimes called dissipative absorption).
-
Resonant frequency
The resonance frequencies of an atom are those frequencies which correspond via E = hν to energies at which the electron can make jumps between quantized energy states. At these frequencies, light is likely to be absorbed by atoms. Confusingly, the natural frequency at which electrons in an atom can vibrate as atomic dipoles, given by σ0 =
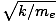 is also sometimes called the resonant frequency. A
forced oscillation will be most effective when it is close to the resonant frequency.
is also sometimes called the resonant frequency. A
forced oscillation will be most effective when it is close to the resonant frequency.
Terms
Formulae
| Wave Equation |
|
| Maxwell's Equation |
|
| Poynting Equation |
|
| Light Equation |
|


 payment page
payment page
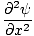 =
= 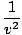
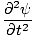
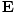
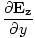 -
- 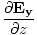 )
) + (
+ (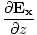 -
-  )
)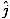 + (
+ (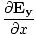 -
- 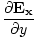 )
)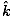
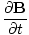
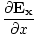 +
+ 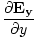 +
+ 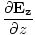 = 0
= 0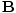
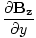 -
- 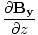 )
)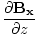 -
- 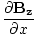 )
)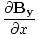 -
-  )
)
 +
+ 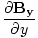 +
+ 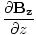 = 0
= 0


