Terms
-
Oscillating system
Any system that always experiences a force acting against the
displacement of
the system (restoring force).
-
Restoring force
A force that always acts against the displacement of the system.
-
Periodic Motion
Any motion in which a system returns to its initial position at a later
time.
-
Amplitude
The maximum displacement of an oscillating system.
-
Period
The time it takes for a system to complete one oscillation.
-
Frequency
The rate at which a system completes an oscillation.
-
Hertz
The unit of measurement of frequency.
-
Angular Frequency
The radian measure of frequency: frequency times 2Π.
-
Simple Harmonic Motion
Any motion that experiences a restoring force proportional to the
displacement of the system.
-
Torsional Oscillator
The oscillation of any object suspended by a wire and rotating about
the axis of the wire.
-
Pendulum
The classic pendulum consists of a particle suspended from a light
cord. When the particle is pulled to one side and released, it swings
back past the equilibrium point and oscillates between two maximum
angular displacements.
-
Damping force
A force proportional to the velocity of the object that causes it to
slow down.
-
Resonance
The phenomena in which a driving force causes a rapid increase in the
amplitude of
oscillation of a system.
-
Resonant Frequency
The frequency at which a driving force will produce resonance in a given oscillating
system.
Formulae
|
Relation between variables of oscillation
| σ = 2Πν = 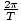 |
|
Force exerted by a spring with constant k | F = - kx |
|
Differential equation describing simple harmonic motion
| 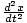 + + 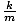 x = 0 x = 0 |
|
Formula for the period of a mass-spring system
| T = 2Π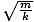 |
|
Formula for the frequency of a mass-spring system
| ν =  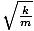 |
|
Formula for the angular frequency of a mass-spring system
| σ = 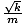 |
|
Equation for the displacement in simple harmonic motion
| x = xmcos(σt) |
|
Equation for the velocity in simple harmonic motion
| v = σxmsin(σt) |
|
Equation for the acceleration in simple harmonic motion
| a = σ2xmcos(σt) |
|
Equation for the potential
energy of a
simple
harmonic system
| U = 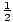 kx2 kx2 |
|
Equation for the torque felt in a torsional oscillator
| τ = - κσ |
|
Equation for angular displacement of a torsional oscillator
| θ = θmcos(σt) |
|
Equation for the period of a torsional oscillator
| T = 2Π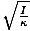 |
|
Equation for the angular frequency of a torsional oscillator
| σ = 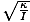 |
|
Equation for the force felt by a pendulum
| F = mg sinθ |
|
Approximation of the force felt by a pendulum
| F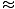 - ( - (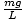 )x )x |
|
Equation for the period of a pendulum
| T = 2Π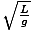 |
|
Differential equation describing damped motion
| kx + b + m + m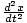 = 0 = 0 |
|
Equation for the displacement of a damped system
| x = xme cos(σâ≤t) cos(σâ≤t) |
|
Equation for the angular frequency of a damped system
| σâ≤ = 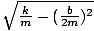 |
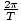
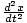 +
+ 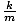 x = 0
x = 0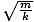

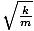
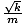
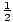 kx2
kx2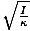
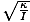
 - (
- (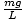 )x
)x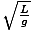
 + m
+ m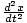 = 0
= 0 cos(σâ≤t)
cos(σâ≤t)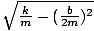


 payment page
payment page



