Concepts
This section is really an extension of 4-vectors which introduced the energy-momentum 4-vector. Here we see how the concept of a 4-vector, in particular the fact that the inner product is invariant between frames, can be applied to solve problems involving collisions and decays. Many such particle-particle collisions occur on the atomic or sub-atomic level; such small particles require little (by macroscopic standards) energy to accelerate them to speeds near the speed of light. Thus, Special Relativity is necessary for describing many of these interactions.
Recall that the energy-momentum 4-vector or 4-momentum is given by:
PâÉá(E/c,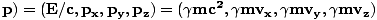 |
The total energy and momentum of a number of particles is just the sum of their individual 4-momenta. If the total 4-momenta before a collision or decay is Pi and the total 4-momenta after is Pf the conservation of energy and momentum are both expressed in the equation Pi = Pf. Given the definition of the inner product from properties in dynamics, it is easy to see that:
P2âÉáP.P = E2/c2 - | |
This is the most important relationship in the section.
Examples
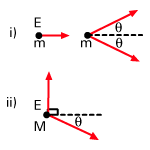
Now let us tackle an example of first a collision problem and then a decay problem. Consider a particle with
energy E and mass m. This particle moves towards another identical particle at rest. The particles
collide elastically and both scatter at an angle θ with respect to the incident direction. This is
illustrated in .
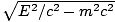 . The 4-mometa after the collision are: P1' = (E'/c, p'cosθ, p'sinθ, 0)
and P2' = (E'/c, p'cosθ, - p'sinθ, 0), where p' =
. The 4-mometa after the collision are: P1' = (E'/c, p'cosθ, p'sinθ, 0)
and P2' = (E'/c, p'cosθ, - p'sinθ, 0), where p' = 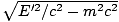 . We know from the
symmetry of the situation that the energy and momentum of the two particles must be equal after the
collision. Conserving energy gives E' =
. We know from the
symmetry of the situation that the energy and momentum of the two particles must be equal after the
collision. Conserving energy gives E' = 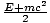 . Conserving momentum (only the x-
direction is significant since the y components cancel) gives: p'cosθ = p/2. Thus:
. Conserving momentum (only the x-
direction is significant since the y components cancel) gives: p'cosθ = p/2. Thus:
P1' = 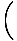  , ,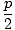 , ,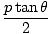 , 0 , 0 |
But we can take the inner product of this with itself and set it equal to m2c2:
| m2c2 | = | 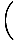   - -  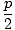 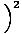 (1 + tan2θ) (1 + tan2θ) | |
| âá’4m2c4 | = | (E + mc2)2 -  | |
| âá’E2 + m2c4 +2Emc2 -4m2c4 | = |  | |
| âá’cos2θ | = | 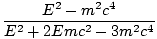 = = 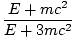 |
Which is the result desired.
Decay problems can be solved in a similar manner; that is, by conserving energy and momentum. The
situation in which a particle of mass M and energy E decays into two identical particles is also shown in
. As shown, one particle heads off in the y-direction, and the other at an
angle θ. Our problem is to calculate the energies of these particles resulting from the decay. Again,
we begin by writing down the 4-momenta before and after the collision. Before the decay P = (E/c,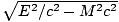 , 0, 0) and after P1 = (E1/c, 0, p1, 0) and P2 = (E2/c, p2cosθ, - p2sinθ, 0); if the created particles have mass m, then, p1 =
, 0, 0) and after P1 = (E1/c, 0, p1, 0) and P2 = (E2/c, p2cosθ, - p2sinθ, 0); if the created particles have mass m, then, p1 = 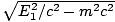 and
p2 =
and
p2 = 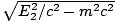 . This problem becomes quite algebraically messy if we proceed in the
same manner as we did above, conserving energy and momentum. Instead let us exploit
the invariance of the inner product to solve the problem. Conservation of energy and momentum tells us
that P = P1 + P2 which implies P2 = P - P1. Taking inner products we have:
. This problem becomes quite algebraically messy if we proceed in the
same manner as we did above, conserving energy and momentum. Instead let us exploit
the invariance of the inner product to solve the problem. Conservation of energy and momentum tells us
that P = P1 + P2 which implies P2 = P - P1. Taking inner products we have:
| (P - P1).(P - P1) = P2.P2 | |||
| âá’P2 -2P.P1 + P12 = P22 | |||
| âá’M2c2 -2EE1/c2 + m2c2 = m2c2 | |||
âá’E1 = 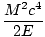 |
We have made good use of the fact that the inner product of any 4-momenta with itself is just m2c2. To get E2 we apply conservation of energy to deduce that E1 + E2 = Eâá’E2 = E - E1 =
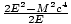 . Solving the problem in this way gets rid of the messiness of P2.
. Solving the problem in this way gets rid of the messiness of P2.


 payment page
payment page



