Relativistic Momentum
In this setion we will turn to a discussion of some interesting aspects of Special Relativity, concerning how particle and objects gain motion, and how they interact. In this section we will arrive at an expression that looks something like the definition of momentum, and seems to be a conserved quantity under the new rules of Special Relativity. With this in mind consider the following setup.
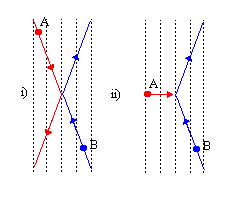
If the y-velocity is much greater than the x-velocity, then particle A is essentially at rest with respect to
particle B in A's frame. Time
dilation
tells us that particle B's clock must be
running slow by a factor 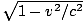 . Particle B's clock ticks once for every vertical line crossed
(independent of frame), so particle B must be moving more slowly than A in the x-direction by a factor
. Particle B's clock ticks once for every vertical line crossed
(independent of frame), so particle B must be moving more slowly than A in the x-direction by a factor 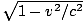 . Thus the magnitudes of the x-velocities of the particles are not the same. This means that the
Newtonian px = mvx is not a conserved quantity because the momentum of particle B would be smaller than the
momentum of particle A by the factor 1/γ since | vx| is larger for particle A. We have shown that if
momentum is to be conserved, the momenta of A and B better be the same. However, the solution to the difficulty is
not so hard: we define momentum as:
. Thus the magnitudes of the x-velocities of the particles are not the same. This means that the
Newtonian px = mvx is not a conserved quantity because the momentum of particle B would be smaller than the
momentum of particle A by the factor 1/γ since | vx| is larger for particle A. We have shown that if
momentum is to be conserved, the momenta of A and B better be the same. However, the solution to the difficulty is
not so hard: we define momentum as:
px = γmvx =  |
A is at rest in the y-direction so γA = 1, and mvx = γmvx. For B however, this we have exactly taken care of the problem: the factor by which particle B's speed was smaller is canceled out by the γ so particle B also has momentum px =
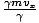 = mvx.
= mvx.
In three dimensions the equation for relativistic momentum becomes:
 |
We have not shown here that γmv is conserved--this is the job of experiments. What we have done is to provide some motivation for the equation for relativistic momentum by showing that γm
 (or some constant multiple of it) is the only vector of this form which has any chance of
being conserved in a collision (for instance, γ2m
(or some constant multiple of it) is the only vector of this form which has any chance of
being conserved in a collision (for instance, γ2m we now know, is certainly not
conserved).
we now know, is certainly not
conserved).
Relativistic Energy
To develop a concept of relativistic energy we will again consider a scenario and show that a particular
expression is conserved. This expression we just happen to give the label 'energy.'
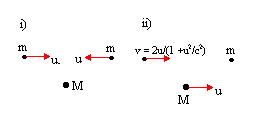
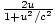 . The γ factor associated
with v is γv =
. The γ factor associated
with v is γv = 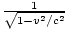 =
= 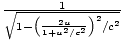 =
= 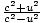 . In this frame conservation of
momentum gives:
. In this frame conservation of
momentum gives:
γvmv + 0 = γMuâá’m 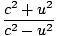   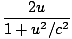  = = 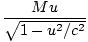 âá’M = âá’M = 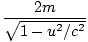 |
Surprisingly, M is not equal to 2m, but is larger by a factor γ. However, in the limit u < < c, M
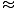 2m as expected from the correspondence
principle.
2m as expected from the correspondence
principle.
Let us now state the expression for relativistic energy and check whether it is conserved:
| EâÉáγmc2 |
If γmc2 is conserved then:
| γvmc2 +1×mc2 | = | γuMc2âá’ 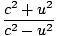  m + m m + m | |
| = | 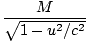 âá’ âá’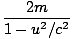 | ||
| = | 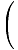 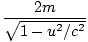  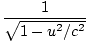 |
This last equality is clearly true. Thus we have found a quantity that looks a little bit like classical energy and is conserved in collisions. What happens in the limit v < < c? We can use the binomial series expansion to expand (1 - v2/c2)-1/2 as follows:
| EâÉáγmc2 | = | 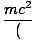 1 - v2/c2)-1/2 1 - v2/c2)-1/2 | |
| = | mc2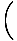 1 + 1 +  + +  + +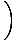 | ||
| = | mc2 + 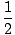 mv2 + mv2 + |
The higher order terms can be neglected for v < < c. First note that for v = 0 the second (and all higher) terms are zero so we have the famous E = mc2 for a particle at rest. Second, mc2 is just a constant so conservation of energy reduces to the conservation of mv2/2 in this limit. Moreover, the reduction of E = γmc2 to the Newtonian form in this limit justifies our choice of γmc2 rather that say, 5γmc8 as our expression for energy.


 payment page
payment page



