Although the use of 4-vectors is not necessary for a full understanding of Special Relativity, they are a most powerful and useful tool for attacking many problems. A 4-vectors is just a 4-tuplet A = (A0, A1, A2, A3) that transforms under a Lorentz Transformation in the same way as (cdt, dx, dy, dz) does. That is:
| A0 = γ(A0' + (v/c)A1') | |||
| A1 = γ(A1' + (v/c)A0') | |||
| A2 = A2' | |||
| A3 = A3' |
As we saw in the minkowski diagrams, Lorentz transformations are very much like rotations in 4-dimensional spacetime. 4-vectors, then, generalize the concept of rotations in 3-space to rotations in 4-dimensions. Clearly, any constant multiple of (cdt, dx, dy, dz) is a 4-vector, but something like A = (cdt, mdx, dy, dz) (where m is just a constant) is not a 4-vector because the second component has to transform like mdxâÉáA1 = γ(A1' + (v/c)A0')âÉáγ((mdx') + vdt') from the definition of a 4-vector, but also like mdx = mγ(dx' + (v/c)dt'); these two expression are inconsistent. Thus we can transform a 4-vector either according to the 4- vector definition given above, or using what we know about how the dxi transform to transform each Ai independently. There are only a few special vectors for which these two methods yield the same result. Several different 4-vectors are now discussed:
Velocity 4-vector
We can define a quantity τ =  which is called the proper time, and
is invariant between frames. Dividing out original 4-vector ((cdt, dx, dx, dz)) by dτ gives:
which is called the proper time, and
is invariant between frames. Dividing out original 4-vector ((cdt, dx, dx, dz)) by dτ gives:
V = 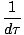 (cdt, dx, dy, dz) = γ (cdt, dx, dy, dz) = γ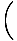 c, c,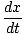 , ,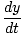 , ,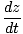 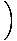 = (γc, γ = (γc, γ |
This arises because
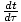 = γ.
= γ.
Energy-momentum 4-vector
If we multiply the velocity 4-vector by m we get:
P = mV = m(γc, γ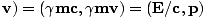 |
This is an extremely important 4-vector in Special Relativity.
Properties of the 4-vector
What gives 4-vectors their usefulness in Special Relativity is their many nice properties. First, they are linear: if A and B are 4-vectors and a and b are any constants, then C = aA + bB is also a 4-vector. Even more importantly, 4-vectors have inner product invariance. We define the inner product of two 4-vectors A and B to be:
A.BâÉáA0B0 - A1B1 - A2B2 - A3B3âÉáA0B0 - 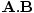 |
It is not hard to verify by direct computation that this inner product is the same no matter which frame it is calculated . This is a crucial result. Just as the usual dot product is invariant under rotations in 3-dimensions, the inner product defined here is invariant under rotations in our 4-space. The unusual minus signs arise because of the form of the Lorentz Transformations; this is just the way the math comes out in order for the inner product of two 4-vectors to be invariant under the Lorentz Transformations. We can also use this inner product to define the norm, or length, of a 4-vector as:
| | A|2âÉáA.A = A0A0 - A1A1 - A2A2 - A3A3 = A02 - | bfA|2 |
We can now begin to see the usefulness of 4-vectors: they can, given an arbitrary combination of 4-vectors, we can immediately produce a quantity that is independent of reference frame, enabling us to draw immediate conclusions about what is going on in the particular frame we are interested in. One example is that if we take the combination P.P, the inner product of the momentum 4-vector with itself we have P.P = E2/c2 - |
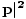 , which we know must be invariant. However, it is not obvious what constant value this is. But the invariance of the
4-vector allows us to choose any frame; we can choose the one where
, which we know must be invariant. However, it is not obvious what constant value this is. But the invariance of the
4-vector allows us to choose any frame; we can choose the one where  . Here the
inner product becomes P.P = E2/c2. But for a particle at rest we know E = mc2, thus E2/c2 = m2c2 and hence P.P = E2 - c2|
. Here the
inner product becomes P.P = E2/c2. But for a particle at rest we know E = mc2, thus E2/c2 = m2c2 and hence P.P = E2 - c2|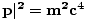 in every frame. Thus we have
derived the same relationship between momentum and energy that we saw in Section 1, this
time by using inner product invariance.
in every frame. Thus we have
derived the same relationship between momentum and energy that we saw in Section 1, this
time by using inner product invariance.


 payment page
payment page



