Time Dilation
The most important and famous results in Special Relativity are that of time dilation and length contraction. Here we will proceed by deriving time dilation and then deducing length contraction from it. It is important to note that we could do it the other way: that is, by beginning with length contraction.
tA = 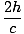 |
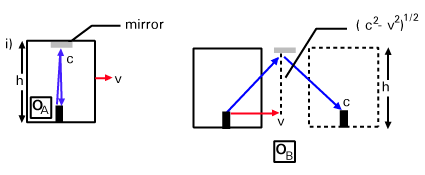
In the frame of an observer on the ground, call her OB, the train is moving with speed v (see ii) in ). The light then follows a diagonal path as shown, but still with speed c. Let us calculate the length of the upward path: we can construct a right-triangle of velocity vectors since we know the horizontal speed as v and the diagonal speed as c. Using the Pythagorean Theorem we can conclude that the vertical component of the velocity is
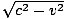 as shown on the diagram. Thus
the ratio the diagonal (hypotenuse) to the vertical is
as shown on the diagram. Thus
the ratio the diagonal (hypotenuse) to the vertical is 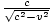 . But we know that the
vertical of the right-triangle of lengths is h, so the hypotenuse, must have length
. But we know that the
vertical of the right-triangle of lengths is h, so the hypotenuse, must have length 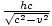 . This is the length of the upward path. Thus the overall length of the path taken by the light in
OB's frame is
. This is the length of the upward path. Thus the overall length of the path taken by the light in
OB's frame is 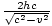 . It traverses this path at speed c, so the time taken is:
. It traverses this path at speed c, so the time taken is:
tB = 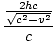 = = 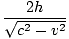 |
Clearly the times measured are different for the two observers. The ratio of the two times is defined as γ, which is a quantity that will become ubiquitous in Special Relativity.
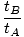 = γâÉá = γâÉá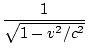 |
All this might seem innocuous enough. So, you might say, take the laser away and what is the problem? But time dilation runs deeper than this. Imagine OA waves to OB every time the laser completes a cycle (up and down). Thus according to OA's clock, he waves every tA seconds. But this is not what OB sees. He too must see OA waving just as the laser completes a cycle, however he has measured a longer time for the cycle, so he sees OA waving at him every tB seconds. The only possible explanation is that time runs slowly for OA; all his actions will appear to OB to be in slow motion. Even if we take the laser away, this does not affect the physics of the situation, and the result must still hold. OA's time appears dilated to OB. This will only be true if OA is stationary next to the laser (that is, with respect to the train); if he is not we run into problems with simultaneity and it would not be true that OB would see the waves coincide with the completion of a cycle.
Unfortunately, the most confusing part is yet to come. What happens if we analyze the situation from
OA's point of view: he sees OB flying past at v in the backwards direction (say OB has a laser
on the ground reflecting from a mirror suspended above the ground at height h). The relativity
principle tells us that the same reasoning must apply and thus that OA observes OB's clock
running slowly (note that γ does not depend on the sign of v). How could this possibly be right?
How can OA's clock be running slower than OB's, but OB's be running slower than OA's?
This at least makes sense from the point of view of the relativity principle: we would expect from the
equivalence of all frames that they should see each other in identical ways. The solution to this mini-paradox
lies in the caveat we put on the above description; namely, that for tB = γtA to hold, OA
must be at rest in her frame. Thus the opposite, tA = γtB, must only hold when OB is at
rest in her frame. This means that tB = γtA holds when events occur in the same place in
OA frame, and tA = γtB holds when events occur in the same place in OB's frame.
When v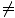 0âá’γ
0âá’γ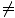 1 this can never be true in both frames at once, hence only one
of the relations holds true. In the last example described (OB flying backward in OA's frame), the
events (laser fired, laser returns) do not occur at the same place in OA's frame so the first relation we
derived (tB = γtA) fails; tA = γtB is true, however.
1 this can never be true in both frames at once, hence only one
of the relations holds true. In the last example described (OB flying backward in OA's frame), the
events (laser fired, laser returns) do not occur at the same place in OA's frame so the first relation we
derived (tB = γtA) fails; tA = γtB is true, however.
Length Contraction
We will now proceed to derive length contraction given what we know about time dilation. Once again
observer OA is on a train that is moving with velocity v to the right (with respect to the ground). OA
has measured her carriage to have length lA in her reference frame. There is a laser light on the back
wall of the carriage and a mirror on the front wall, as shown in .
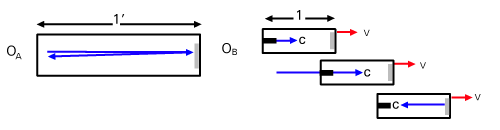
tA = 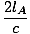 |
Since the light traverses the length of the carriage twice at velocity c. We want to compare the length as observed by OA to the length measured by an observer at rest on the ground (OB). Let us call the length OB measures for the carriage to be lB (as far as we know so far lB could equal lA, but we will soon see that it does not). In OB's frame as the light is moving towards the mirror the relative speed of the light and the train is c - v; after the light has been reflected and is moving back towards OA, the relative speed is c + v. Thus we can calculate the total time taken for the light to go up and back as:
tB = 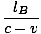 + + 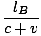 = = 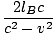 âÉá âÉá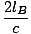 γ2 γ2 |
But from our analysis of time dilation above, we saw that when OA is moving past OB in this manner, OA's time is dilated, that is: tB = γtB. Thus we can write:
γtA = γ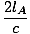 = tB = = tB = 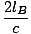 γ2âá’ γ2âá’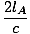 = = 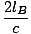 γâá’lB = γâá’lB = 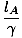 |
Note that γ is always greater than one; thus OB measures the train to be shorter than OA does. We say that the train is length contracted for an observer on the ground.
Once again the problem seems to be that is we turn the analysis around and view it from OA's point of view: she
sees OB flying past to the left with speed v. We can put OB in an identical (but motionless) train and apply
the same reasoning (just as we did with time dilation) and conclude that OA measures OB's identical carriage to
be short by a factor γ. Thus each observer measures their own train to be longer than the other's. Who is right? To
resolve this mini-paradox we need to be very specific about what we call 'length.' There is only one meaningful definition of
length: we take object we want to measure and write down the coordinates of its ends simultaneously and take the
difference. What length contraction really means then, is that if OA compares the simultaneous coordinates of his own
train to the simultaneous coordinates of OB's train, the difference between the former is greater than the difference between
the latter. Similarly, if OB writes down the simultaneous coordinates of his own train and OA's, he will find the
difference between his own to be greater. Recall from Section
1 that
observers in
different frames have different notions of simultaneous. Now the 'paradox' doesn't seem so surprising at all; the times
at which OA and OB are writing down their coordinates are completely different. A simultaneous measurement for
OA is not a simultaneous measurement for OB, and so we would expect a disagreement as to the observers concept of
length. When the ends are measured simultaneously in OB's frame lB = 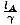 , and when events are measured
simultaneously in OA's frame lA =
, and when events are measured
simultaneously in OA's frame lA = 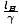 . No contradiction can arise because the criterion of simultaneity
cannot be met in both frames at once.
. No contradiction can arise because the criterion of simultaneity
cannot be met in both frames at once.


 payment page
payment page



