Examples of Recursion: Problems 5

Problem : Write a function that does a post-order traversal of a tree and returns the sum of the data in all the nodes it visits.

int sum_postorder(tree_t *tree) { if (tree!=NULL) return tree->data + sum_postorder(tree->left) + sum_postorder(tree->right); else return 0; }

Problem : Write a function to find the minimum height of the tree, meaning the path from the root to a NULL child that passes through the fewest nodes.

int tree_min_height(tree_t *tree) { int left, right; if (tree==NULL) { return 0; } else { left = tree_min_height(tree->left); right = tree_min_height(tree->right); return(1 + (left > right ? right : left)); } }

Problem : Write a function that finds the largest value in a tree containing an unsigned integer as the data.

unsigned int tree_max_val(tree_t *tree) { if (tree==NULL) return 0; else { unsigned int left = tree_max_val(tree->left); unsigned int right = tree_max_val(tree->right); unsigned int max = left > right ? left : right; max = tree->data > max ? tree->data : max; return max; } }

Problem : Imagine that you were to draw a tree on a piece of paper, cut it out, and then connect it together with wire and string like it was a mobile. In more technical terms, the tree's right and left child would be allowed to swap places, taking with them their children. Write a function to compare two mobile trees to determine their equality. The following are examples of mobile and non-mobile trees.

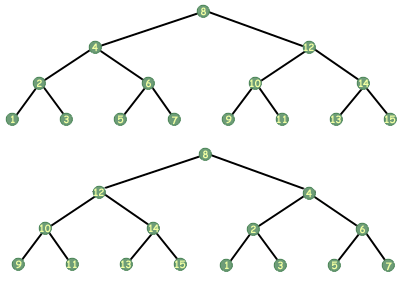
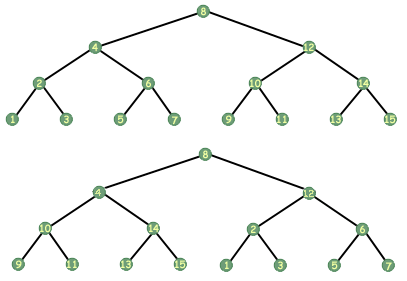
int mobile_trees(tree_t *tree1, tree_t *tree2) { if (tree1==NULL || tree2==NULL) return(tree1 == tree2); else if (tree1->data != tree2->data) return 0; /* not equal */ else return((mobile_trees(tree1->left, tree2->left) && mobile_trees(tree1->right, tree2->right)) || (mobile_trees(tree1->left, tree2->right) && mobile_trees(tree1->right, tree2->left))); }

Problem : CHALLENGE: This question's difficulty represents the power of recursion. How would you write a function to do a pre-order traversal of a tree? Recursively, right? Now, can you think of a way to write a function that would do an iterative traversal of a tree? The catch: you can only use a constant amount of memory (this means you can't have a dynamic array of pointers or a linked list or anything like that), and when the function ends, the tree must be intact (in other words, if you modify the tree, you need to put it back to the way it was). Don't worry if you can't get this one right off the bat. Also, don't attempt to write the code for this function; you'll most likely use a good amount of ink.

The problem you most likely faced when thinking about this is how to get back up a path in the tree once you've gone down it; after all, with a constant amount of memory and without recursion you are unable to keep a stack of all the parents in order to traverse backwards. How do you overcome this? We modify the tree on the way down, and put it back the way it was on the way up. We use three pointers: a previous pointer, a current pointer, and a next pointer. On the way down, we set the current pointer's next field (which is the same as the next pointer) to be the value of the previous pointer. On our way down, this creates a linked list of nodes that goes back up the tree. On the way up, we change the tree back to the way it was. Draw this out and play with it to convince yourself that it works. The same principle can be used to traverse a singly-linked list in both directions.