Examples of Recursion: Recursion on Numbers

There exist many opportunities to use recursive techniques when doing numerical computation.

Printing an Integer

Suppose you wanted to print out an integer. How would you do it? Your first response would probably be that you would use printf. But what if printf didn't exist? What if you were actually responsible for writing the code for printf to print out an integer? Enter recursion.

One way to implement printf's integer printing facilities would be to use the modulo and division operators to look at each digit of the integer. For example, let's use the number 214. To get the first digit, we do 214%10 which results in the digit in the 10s place, 4. We then divide 214 by 10 to get 21. Now we repeat. We mod 21 by 10 and get 1; divide 21 by 10 and get 2. Now we repeat. We mod 2 by 10 and get 2; divide 2 by 10 and get 0. Now that we've reached 0, we're done. A problem with this solution, however, is that we've received the digits in reverse order. One way to fix this would be to use an array to store each of the digits as we receive them, and then iterate through the array in the reverse order, printing out the digits as we go.

void print_int(int num) { int len = 0; int digits[100]; /* 100 digit limit */ for(len=0; len < 100 && num!=0; len++) { digits[len] = num % 10; num /= 10; } for(; len >= 0; len--) putchar('0' + digits[len]); }

Note: The putchar('0' + digits[len]) might look slightly strange, but it works. The putchar() function writes a single character to stdout. By adding a digit to '0' we're converting a digit to its character equivalent. In other words, '0' + 2 == '2' and '0' + 9 == '9'.

The above method works, but it is much more complicated then need be. Believe it or not (and you will after seeing it below), we can write the same function using recursion in only two lines, and no extra variables. So let's think about this recursively.

What is our small problem? We know how to print out a single digit: putchar(num % 10 + '0'), right?

If our number is only a single digit, then the number divided by 10 will be 0. So we just print out the digit, and we're done. What if our number is two digits? How do we turn it into a single digit problem? We'd need to somehow store the current number (so we could come back to it) and then divide it by 10; now we're back at the single digit problem we know how to solve. If we then go back to the two digit number we saved, we can print out the other digit just by modding it by 10. Get the idea? We'll use recursion to serve the purpose of the array, allowing us to go backwards.

void print_int(int num) { if (num / 10) print_int(num / 10); putchar(num % 10 + '0'); }

Cool, huh? This is a good example to show the positives and negatives to recursion. The positives are that this solution is incredibly simple to code and it's easy to look at and understand. It also has the advantage that we don't have to use an array to hold the digits, which means there are no built-in limits to the length of the integer, in digits. The biggest negative is that a function needs to be called for every digit in the number. If the number is long, this can be expensive.

Fibonacci Sequence

Along with the factorial function, another common mathematical function used to teach recursion is the fibonacci function. For those unfamiliar with the fibonacci sequence of numbers, it is achieved by adding the previous two numbers in a sequence to obtain the next number. For example, if the last few numbers in our sequence had been (8,13,21,34,55), the next number would be 89, since 34 + 55 = 89.

The fibonacci sequence can easily be computed recursively. We encounter the base case when the fibonacci number we're looking for is less than or equal to 1, in which case the fibonacci number is 1. The recursive case is when the number in the sequence we're looking for is greater than 1. In that case, it is the sum of the previous two fibonacci numbers:

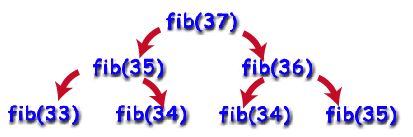
int fib_r(int n) { if (n<=1) return 1; else return(fib_r(n-1) + fib_r(n-2)); }

Unfortunately, this is incredibly inefficient, and is a perfect example of how a recursive solution can be much less efficient than an equivalent iterative solution. Let's say we tried to compute the 37th fibonacci number. To do so, the function would then try to compute the 36th and the 35th fibonacci number. To compute the 36th, it would compute the 34th and the 35th, and to compute that first 35th, it would compute the 33rd and the 34th. Notice that it is doing a lot of extra work here, computing the answer for a number multiple times. In fact, if you were to draw out the tree showing the function calls as is started below, you would notice that there were approximately 2³7 function calls. That's too much for most computers to handle.