Note: This guide is not intended to be an introduction to trees. If you have not yet learned about trees, please see the SparkNotes guide to trees. This section will only briefly review the basic concepts of trees.

What are trees?

A tree is recursive data type. What does this mean? Just as a recursive function makes calls to itself, a recursive data type has references to itself.

Think about this. You are a person. You have all the attributes of being a person. And yet the mere matter that makes you up is not all that determines who you are. For one thing, you have friends. If someone asks you who you know, you could easily rattle off a list of names of your friends. Each of those friends you name is a person in and of themselves. In other words, part of being a person is that you have references to other people, pointers if you will.

A tree is similar. It is a defined data type like any other defined data type. It is a compound data type that includes whatever information the programmer would like it to incorporate. If the tree were a tree of people, each node in the tree might contain a string for a person's name, an integer for his age, a string for his address, etc. In addition, however, each node in the tree would contain pointers to other trees. If one was creating a tree of integers, it might look like the following:

typedef struct _tree_t_ { int data; struct _tree_t_ *left; struct _tree_t_ *right; } tree_t;

Notice the lines struct _tree_t_ *left and struct _tree_t_ *right;. The definition of a tree_t contains fields that point to instances of the same type. Why are they struct _tree_t_ *left and struct _tree_t_ *right instead of what seems to be more reasonable, tree_t *left and tree_t *right? At the point in compilation that the left and right pointers are declared, the tree_t structure has not been completely defined; the compiler doesn't know it exists, or at least doesn't know what it refers to. As such, we use the struct _tree_t_ name to refer to the structure while still inside it.

Some terminology. A single instance of a tree data structure is often referred to as a node. The nodes that a node points to are called children. A node that points to another node is referred to as the child node's parent. If a node has no parent, it is referred to as the root of the tree. A node that has children is referred to as an internal node, while a node that has no children is referred to as a leaf node.

Figure %: Parts of a tree

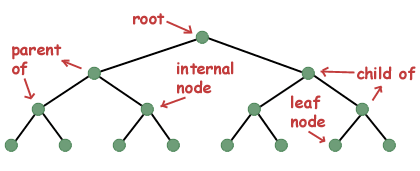
The above data structure declares what's known as a binary tree, a tree with two branches at each node. There are many different kinds of trees, each of which has its own set of operations (such as insertion, deletion, search, etc), and each with its own rules as to how many children a node can have. A binary tree is the most common, especially in introductory computer science classes. As you take more algorithm and data structure classes, you'll probably start to learn about other data types such as red-black trees, b-trees, ternary trees, etc.

As you've probably already seen in previous aspects of your computer science courses, certain data structures and certain programming techniques go hand in hand. For example, you will very rarely find an array in a program without iteration; arrays are far more useful in combination with loops that step through their elements. Similarly, recursive data types like trees are very rarely found in an application without recursive algorithms; these too go hand in hand. The rest of this section will outline some simple examples of functions that are commonly used on trees.

Traversals

As with any data structure that stores information, one of the first things you'd like to have is the ability to traverse the structure. With arrays, this could be accomplished by simple iteration with a for() loop. With trees the traversal is just as simple, but instead of iteration it uses recursion.

There are many ways one can imagine traversing a tree such as the following:

Figure %: Tree to traverse

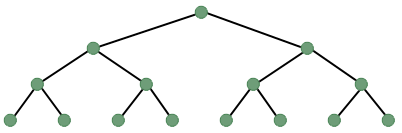
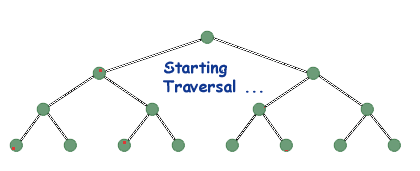
Three of most common ways to traverse a tree are known as in-order, pre-order, and post-order. An in-order traversal is one of the easiest to think about. Take a ruler and place it vertically left of the image of the tree. Now slowly slide it to the right, across the image, while holding it vertically. As it crosses a node, mark that node. An inorder traversal visits each of the nodes in that order. If you had a tree that stored integers and looked like the following:

Figure %: Numbered tree with in-order numerical ordered nodes
an in-order would visit the nodes in numerical order.
Figure %: An in-order traversal of a tree
It may seem that the in-order traversal would be difficult to implement. However, using recusion it can be done in four lines of code.

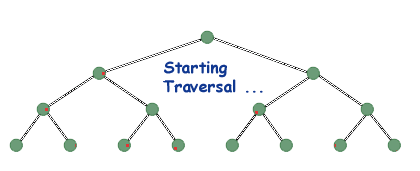
Look at the above tree again, and look at the root. Take a piece of paper and cover up the other nodes. Now, if someone told you that you had to print out this tree, what would you say? Thinking recursively, you might say that you would print out the tree to the left of the root, print out the root, and then print out the tree to the right of the root. That's all there is to it. In an in-order traversal, you print out all of the nodes to the left of the one you're on, then you print yourself, and then you print out all of the ones to the right of you. It's that simple. Of course, that's just the recursive step. What's the base case? When dealing with pointers, we have a special pointer that represents a non-existent pointer, a pointer that points to nothing; this symbol tells us that we should not follow that pointer, that it is null and void. That pointer is NULL (at least in C and C++; in other languages it is something similar, such as NIL in Pascal). The nodes at the bottom of the tree will have children pointers with the value NULL, meaning they have no children. Thus, our base case is when our tree is NULL. Easy.

void print_inorder(tree_t *tree) { if (tree!=NULL) { print_inorder(tree->left); printf("%d\n", tree->data); print_inorder(tree->right); } }

Isn't recursion wonderful? What about the other orders, the pre- and post- order traversals? Those are just as easy. In fact, to implement them we only need to switch the order of the function calls inside the if() statement. In a preorder traversal, we first print ourself, then we print all the nodes to the left of us, and then we print all the nodes to the right of ourself.

Figure %: An pre-order traversal of a tree

And the code, similar to the in-order traversal, would look something like this:

void print_preorder(tree_t *tree) { if (tree!=NULL) { printf("%d\n", tree->data); print_preorder(tree->left); print_preorder(tree->right); } }

In a post-order traversal, we visit everything to the left of us, then everything to the right of us, and then finally ourself.

Figure %: A post-order traversal of a tree

And the code would be something like this:

void print_postorder(tree_t *tree) { if (tree!=NULL) { print_postorder(tree->left); print_postorder(tree->right); printf("%d\n", tree->data); } }

Binary Search Trees

As mentioned above, there are many different classes of trees. One such class is a binary tree, a tree with two children. A well-known variety (species, if you will) of binary tree is the binary search tree. A binary search tree is a binary tree with the property that a parent node is greater than or equal to its left child, and less than or equal to its right child (in terms of the data stored in the tree; the definition of what it means to be equal, less than, or greater than is up to the programmer).

Searching a binary search tree for a certain piece of data is very simple. We start at the root of the tree and compare it to the data element we're searching for. If the node we're looking at contains that data, then we're done. Otherwise, we determine whether the search element is less than or greater than the current node. If it is less than the current node we move to the node's left child. If it is greater than the current node, we move to the node's right child. Then we repeat as necessary.

Binary search on a binary search tree is easily implemented both iteratively and recursively; which technique you choose depends on the situation in which you are using it. As you become more comfortable with recursion, you'll gain a deeper understanding of when recursion is appropriate.

The iterative binary search algorithm is stated above and could be implemented as follows:

tree_t *binary_search_i(tree_t *tree, int data) { tree_t *treep; for (treep = tree; treep != NULL; ) { if (data == treep->data) return(treep); else if (data < treep->data) treep = treep->left; else treep = treep->right; } return(NULL); }

We'll follow a slightly different algorithm to do this recursively. If the current tree is NULL, then the data isn't here, so return NULL. If the data is in this node, then return this node (so far, so good). Now, if the data is less than the current node, we return the results of doing a binary search on the left child of the current node, and if the data is greater than the current node, we return the results of doing a binary search on the right child of the current node.

tree_t *binary_search_r(tree_t *tree, int data) { if (tree==NULL) return NULL; else if (data == tree->data) return tree; else if (data < tree->data) return(binary_search_r(tree->left, data)); else return(binary_search_r(tree->right, data)); }

Sizes and Heights of Trees

The size of a tree is the number of nodes in that tree. Can we write a function to compute the size of a tree? Certainly; it only takes two lines when written recursively:

int tree_size(tree_t *tree) { if (tree==NULL) return 0; else return(1 + tree_size(tree->left) + tree_size(tree->right)); }

What does the above do? Well, if the tree is NULL, then there is no node in the tree; therefore the size is 0, so we return 0. Otherwise, the size of the tree is the sum of the sizes of the left child tree's size and the right child tree's size, plus 1 for the current node.

We can compute other statistics about the tree. One commonly computed value is the height of the tree, meaning the longest path from the root to a NULL child. The following function does just that; draw a tree, and trace the following algorithm to see how it does it.

int tree_max_height(tree_t *tree) { int left, right; if (tree==NULL) { return 0; } else { left = tree_max_height(tree->left); right = tree_max_height(tree->right); return(1 + (left > right ? left : right)); } }

Tree Equality

Not all functions on tree's take a single argument. One could imagine a function that took two arguments, for example two trees. One common operation on two trees is the equality test, which determines whether two trees are the same in terms of the data they store and the order in which they store it.

Figure %: Two equal trees
Figure %: Two unequal trees

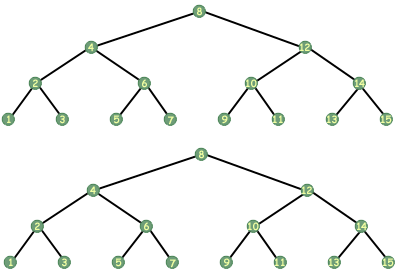
As an equality function would have to compare two trees, it would need to take two trees as arguments. The following function determines whether or not two trees are equal:

int equal_trees(tree_t *tree1, tree_t *tree2) { /* Base case. */ if (tree1==NULL || tree2==NULL) return (tree1 == tree2); else if (tree1->data != tree2->data) return 0; /* not equal */ /* Recursive case. */ else return( equal_trees(tree1->left, tree2->left) && equal_trees(tree1->right, tree2->right) ); }

How does it determine equality? Recursively, of course. If either of the trees is NULL, then for the trees to be equal, both need to be NULL. If neither is NULL, we move on. We now compare the data in the current nodes of the trees to determine if they contain the same data. If they don't we know that the trees are not equal. If they do contain the same data, then there still remains the possibility that the trees are equal. We need to know whether the left trees are equal and whether the right trees are equal, so we compare them for equality. Voila, a recursive tree equality algorithm.

Previous section Next section

Take a Study Break