Fundamentals of the Atom
An atom consists of a nucleus of protons and neutrons, surrounded by electrons. Each of the elements in the periodic table is classified according to its atomic number, which is the number of protons in that element's nucleus. Protons have a charge of +1, electrons have a charge of -1, and neutrons have no charge. Neutral atoms have the same number of electrons and protons, but they can have a varying number of neutrons. Within a given element, atoms with different numbers of neutrons are isotopes of that element. Isotopes typically exhibit similar chemical behavior to each other.
Electrons have such little mass that they exhibit properties of both particles and waves; in. We further know from Heisenberg's Uncertainty Principle that it is impossible to know the precise location of an electron. Despite this limitation, there are regions around the atom where the electron has a high probability of being found. Such regions are referred to as atomic orbitals.
Atomic Orbitals and Quantum Numbers
The relation of a particular electron to the nucleus can be described through a series of four numbers, called the Quantum Numbers. The first three of these numbers describe the energy (Principle quantum number), shape (Angular momentum quantum number), and orientation of the orbital (magnetic quantum number). The fourth number represents the "spin" of the electron (spin quantum number). The four quantum numbers are described below.
Principle Quantum Number (n)
The principle quantum number indicates how the distance of the orbital from the nucleus. Electrons are farther away for higher values of n. Electrons are negatively charged, so electrons that are closer to the positively charged nucleus are more powerfully attracted and tightly bound than those that are farther away. Electrons that are closer to the nucleus are thus more stable, and less likely to be lost by the atom. In other words, as n increases, so does the energy of the electron and the likelihood of that electron being lost by the atom. In a given atom, all the atomic orbitals with the same n are collectively known as a shell. n can take on integer values of 1 or higher (ex. 1, 2, 3, etc.).
Angular Momentum Quantum Number (l)
The angular momentum quantum number describes the shape of the orbital. The
angular momentum number (or subshell) can be represented either by a number
(any integer from 0 up to n-1) or by a letter (s,p,d,f,g, and then up the alphabet), with 0 corresponding to
s, 1 to p, 2 to d, and so on. For example:
when n = 1, l can only equal 0; meaning that shell n = 1
has only an s orbital (l = 0).
when n = 3, l can equal 0, 1, or 2; meaning that shell n =
3 has s,p, and d orbitals.
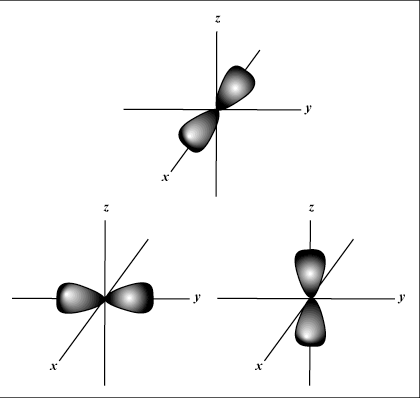
s orbitals are spherical, whereas p orbitals are dumbbell-shaped.
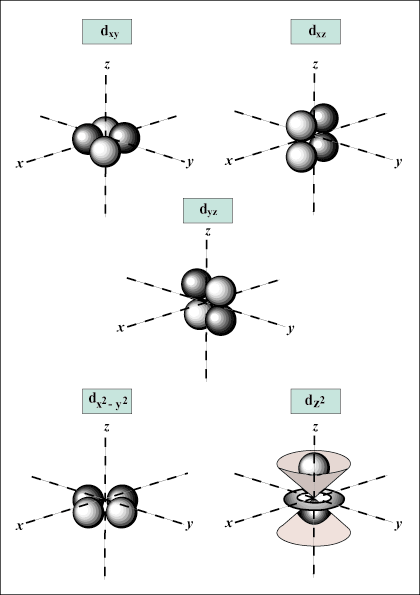
d orbitals and beyond are much harder to visually represent.

Magnetic Quantum Number (m)
Gives the orientation of the orbital in space; in other words, the value of
m describes whether an orbital lies along the x-, y-, or z-axis on a
three-dimensional graph, with the nucleus of the atom at the origin. m
can take on any value from -l to l. For our purposes, it is only
important that this quantum number tells us that for each value of n
there may be up to one s-orbital, three p-orbitals, five d-orbitals, and
so on. For example:
The s orbital (l = 0) has one orbital, since m can only equal 0.
That orbital is spherically symmetrical about the nucleus.