Kinetic Molecular Theory
The most immediately useful bit of information you can pull from the definition of the kinetic molecular theory provided in the summary is that the average kinetic energy of a gas is proportional to the absolute temperature.
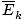 âàùT âàùT |
@@Equation @@ has a number of very serious implications. First of
all, any two gases at the same temperature will have the same kinetic energy.
Remember that kinetic energy Ek = 1/2mv2, and that average kinetic energy
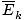 = 1/2m
= 1/2m .
.
Here's where things get complicated. After some mathematical maneuvering we find a more exact expression for the average velocity $\overline{v}$:
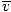 = = 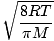 = = 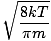 |
k is the Boltzmann constant. Think of the Boltzmann constant as the gas constant R for individual molecules. Analogously, m is the mass per molecule, just as M is the mass per mole. If you multiply k by Avogadro's number, you'll get R.
Let's take a breather. In order to keep things simple, I have refrained from
including derivations. If you are at all mathematically inclined, however, I
suggest that you take a look in a good physics book (look under statistical
mechanics or ideal gases) at the derivations of 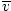 and the other
equations I introduce. Alternatively, ask your instructor to show you. The
derivations can be painful, but they will prove to you that these equations have
meaning.
and the other
equations I introduce. Alternatively, ask your instructor to show you. The
derivations can be painful, but they will prove to you that these equations have
meaning.
Let's get back into the fray. There are two other characterizations of v that you should know: the most probable velocity $v_p$ and the root mean square velocity $v_{\mbox{rms}}$. The most probable velocity is exactly what it sounds like: the velocity at which the greatest number of molecules in a gas travel. It can be expressed mathematically:
vp = 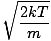 = = 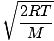 |
The root mean square velocity, which measures the typical velocity of molecules in a gas, is slightly tricky. To derive its value, find the square root of the mean of the squares of the average velocity. It is easier to understand mathematically:
| vrms | = | 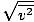 | |
| = | 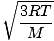 | ||
| = |  |
Make sure that you see that vrms =
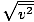 , NOT
vrms =
, NOT
vrms = 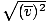 . The latter equation reduces to
vrms =
. The latter equation reduces to
vrms = 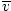 , which is not the case. vrms
requires the mean of the squares of the velocities. Square the velocities
first, then take their mean.
, which is not the case. vrms
requires the mean of the squares of the velocities. Square the velocities
first, then take their mean.
When solving for these values of v, be sure to reduce all variables to SI units. M is particularly insidious--it must be in kg/m3 if all the other units are SI.
Maxwell-Boltzmann Speed Distributions
You'll often see the range of speeds plotted against the number of molecules on
a Maxwell-Boltzmann speed distribution. Plotting the values of
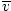 , vp, and vrms, we find that:
, vp, and vrms, we find that:
vp < 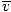 < vrms < vrms |

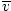 ). The difference between vp and vrms is even
more exaggerated because it involves the mean of squares.
). The difference between vp and vrms is even
more exaggerated because it involves the mean of squares.
A Maxwell-Boltzmann speed distribution changes with temperature. As discussed
with the kinetic molecular theory, higher temperatures lead to higher
velocities. Thus the distribution of a gas at a hotter temperature will be
broader than it is at lower temperatures.

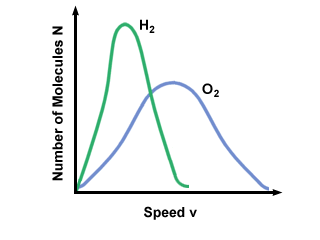
The Maxwell-Boltzmann speed distribution also depends on the molecular mass of
the gas. Heavier molecules have, on average, less kinetic energy at a given
temperature than light molecules. Thus the distribution of lighter molecules
like H2 is much broader and faster than the distribution of a heavier
molecule like O2:
Diffusion and Mean Free Path
Diffusion is the spread of one substance through another. The fact that molecules collide when they diffuse is the reason why it takes a considerable amount of time for a gas to travel from one place to another. Think, for example, of a smell released at one point in the room. Because gas molecules move at such fast velocities, if there were no collisions the smell would fill the room instantly.
The collision between gas molecules makes the calculation of the rate of diffusion difficult. Instead, we'll focus on the mean free path. The mean free path λ is the mean distance a molecule travels before it impacts another molecule; given the huge number of collisions in a gas, the mean free path is vastly smaller than any typical room or container. The mean free path is calculated with the following formula:
λ = 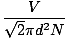 |
N is the total number of molecules present. The rate of collisions is simply vrms divided by the mean free path:
rate of collision = 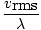 |
Effusion
Effusion is the rate at which a gas passes through a small hole into a vacuum. The rate of effusion of a gas is directly proportional to vrms:
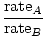 = = 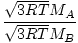 = = 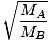 |













