Organic Molecular Orbitals

Valence Bond theory, as we saw in the last section, is based on the notion that electrons are localized to specific atomic orbitals. Molecular orbital theory asserts that atomic orbitals no longer hold significant meaning after atoms form molecules. Electrons no longer "belong", in a sense, to any particular atom but to the molecule as a whole. Molecular orbital theory holds, as its name suggests, that electrons reside in molecular orbitals that are distributed over the entire molecule.

Quantum mechanics specifies that we can get molecular orbitals through a linear combination of atomic orbitals; that is, by adding and subtracting them. How do we add and subtract orbitals? The best way to picture this process is to recall the wave-like nature of electrons. Recall from physics that two waves can interact either through constructive interference, in which the two waves reinforce each other, and destructive interference, in which the two waves cancel each other out. Mathematically, constructive interference corresponds to addition and destructive interference corresponds to subtraction. When atomic orbitals interact, we can either add them to obtain a bonding orbital or subtract them to obtain an antibonding orbital. Antibonding orbitals are denoted with an asterisk (*).

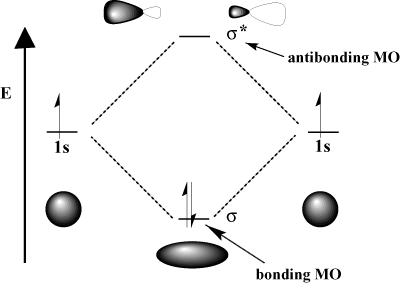
For instance, in the hydrogen molecule, the atomic 1s orbitals can overlap in a σ (head-on) fashion to form a σ-bonding molecular orbital and a σ-antibonding molecular orbital. The bonding molecular orbital is "bonding" in the sense that it is lower in energy than its component atomic orbitals. Forming a bond and moving electrons into the bonding orbital lowers the total energy of the system, which is favorable. On the other hand, moving electrons into the antibonding orbital raises the energy of the system, which disfavors bond formation. The total number of orbitals is conserved; the number of molecular orbitals equals the number of original atomic orbitals.

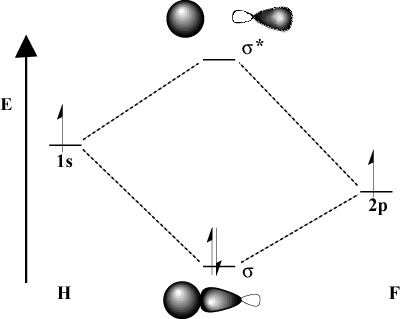
When the bonding atoms significantly differ in electronegativity, their orbital energies will also be different. Compare the MO picture of hydrogen with that of H-F. Because fluorine is more electronegative than hydrogen, its 2p orbitals lie below the 1s orbitals of hydrogen. Due to this difference in energy, the stabilization energy of the resulting bonding MO is not as large. Furthermore, the bonding MO is much more like the 2p orbital in its spatial characteristics while the antibonding MO is much more like the 1s orbital.

One advantage of the MO Model is that it gives us more information about the energies of the bonding electrons. In the case of H₂, the molecule is stabilized by twice the DE of the bonding orbital. The larger this energy gap, the more stable the bond. In order for this stabilization energy to be large, several factors are important:

1. The atoms must be of similar electronegativity.
2. Atoms must be of comparable size.
3. Orbitals must achieve adequate spatial overlap.

For example, the fact that the O-H bond is stronger than the S-H bond can be explained by item 2. The 2p orbital of oxygen can overlap with the 1s orbital of hydrogen more effectively than it can with the 3p orbital of sulfur. Finally, item 3 correctly predicts that σ bonds should be stronger than π bonds since they have a greater degree of direct overlap.

How does MO theory describe multiple bonds? In MO theory the bond order of a bond is the number of bonding electron pairs minus the number of antibonding electron pairs. Intuitively, bonding electrons stabilize the bond while antibonding electron destabilize the bond. The greater this difference, the stronger the bond, and the higher the bond order. As we'll see, in MO theory the bond order is no longer limited to integer values.

One of the greatest successes of MO theory is that it accounts for electron delocalization in a natural way. We have seen that some molecules require resonance structures to be represented accurately. In all such cases, electrons are delocalized over several bonds/atoms. One main drawback of the VB model is that it assigns electrons to specific atoms/bonds and therefore breaks down when it comes to explaining delocalized electrons. The MO model has no such problem; it offers a clean approach to describing delocalization that is superior to writing a bunch of awkward resonance structures.

Unfortunately, the complexity of the full MO model increases exponentially with the size of the molecule. In order for MO theory to be useful in practice, we limit its application to portions of a molecule that are extensively delocalized. This often occurs when π electrons and lone pairs overlap over several contiguous atoms.

Let us once again consider benzene, the classic example of resonance. Recall that benzene consists of six identical C-C bonds each with a bond order of 1 1/2. In order to gain a reasonably simple MO treatment of benzene, the key is to consider the π framework separately from the σ framework. We can assume that the σ bonds are fairly localized and are accurately described by the VB Model. The six π electrons can be considered in a separate MO scheme without much loss of accuracy and predictive power.