Please wait while we process your payment
If you don't see it, please check your spam folder. Sometimes it can end up there.
If you don't see it, please check your spam folder. Sometimes it can end up there.
Please wait while we process your payment
Get instant, ad-free access to our grade-boosting study tools with a 7-day free trial!
Learn more



This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Create Account
Select Plan
Payment Info
Start 7-Day Free Trial!

Annual
2-49 accounts
$22.49/year + tax
50-99 accounts
$20.99/year + tax
Select Quantity
Price per seat
$29.99 $--.--
Subtotal
$-.--
Want 100 or more? Request a customized plan
You could save over 50%
by choosing an Annual Plan!

SAVE OVER 50%
compared to the monthly price!
| Focused-studying | ||
| PLUS Study Tools | ||
| AP® Test Prep PLUS | ||
| My PLUS Activity | ||
$22.49/month + tax
Save 25%
on 2-49 accounts
$20.99/month + tax
Save 30%
on 50-99 accounts
| Focused-studying | ||
| PLUS Study Tools | ||
| AP® Test Prep PLUS | ||
| My PLUS Activity | ||
No Fear provides access to Shakespeare for students who normally couldn’t (or wouldn’t) read his plays. It’s also a very useful tool when trying to explain Shakespeare’s wordplay!
Erika M.
I tutor high school students in a variety of subjects. Having access to the literature translations helps me to stay informed about the various assignments. Your summaries and translations are invaluable.
Kathy B.
Teaching Shakespeare to today's generation can be challenging. No Fear helps a ton with understanding the crux of the text.
Kay H.
No Fear provides access to Shakespeare for students who normally couldn’t (or wouldn’t) read his plays. It’s also a very useful tool when trying to explain Shakespeare’s wordplay!
Erika M.
I tutor high school students in a variety of subjects. Having access to the literature translations helps me to stay informed about the various assignments. Your summaries and translations are invaluable.
Kathy B.
Teaching Shakespeare to today's generation can be challenging. No Fear helps a ton with understanding the crux of the text.
Kay H.
Create Account
Select Plan
Payment Info
Start 7-Day Free Trial!
You will only be charged after the completion of the 7-day free trial.
If you cancel your account before the free trial is over, you will not be charged.
You will only be charged after the completion of the 7-day free trial. If you cancel your account before the free trial is over, you will not be charged.
Order Summary
Annual
7-day Free Trial
SparkNotes PLUS
$29.99 / year
Annual
Quantity
51
PLUS Group Discount
$29.99 $29.99 / seat
Tax
$0.00
SPARK25
-$1.25
25% Off
Total billed on Nov 7, 2024 after 7-day free trail
$29.99
Total billed
$0.00
Due Today
$0.00
Promo code
This is not a valid promo code
Card Details
By placing your order you agree to our terms of service and privacy policy.
By saving your payment information you allow SparkNotes to charge you for future payments in accordance with their terms.
Powered by stripe
Legal
Google pay.......



Please wait while we process your payment

Sorry, you must enter a valid email address
By entering an email, you agree to our privacy policy.
Please wait while we process your payment

Sorry, you must enter a valid email address
By entering an email, you agree to our privacy policy.
Please wait while we process your payment

Your PLUS subscription has expired
Please wait while we process your payment
Please wait while we process your payment

Solution Composition
A solution is a homogeneous mixture. That means the components of a solution are so evenly spread throughout the mixture that there are no perceivable differences in composition. Solutions can be formed by mixing two substances together such as sugar and water. If you pour a packet of sugar into a glass of water, initially you have a suspension as the sugar crystals float about in the glass. When you have stirred the sugar and water for long enough, you will eventually get a clear, colorless mixture. Some people, especially young children, can be fooled by such a demonstration into thinking that the sugar has "disappeared". However, as chemists, we know better. The law of conservation of matter states that the sugar can not just disappear, it must have gone somewhere else. That somewhere else is into solution. The sugar has become evenly dispersed. In fact the sugar molecules are so well spread out that we can no longer see a single sugar crystals. However, if you taste the water, you will find it to be sugary--confirming the presence of sugar in the water. The minor component of the solution is called the solute. In the present example, sugar is the solute. The major component of the solution is called the solvent. In this case water is the solvent.
Solutions can also be formed by mixing together many different phases of matter. For instance, air is a solution. The solute gasses oxygen, carbon dioxide, argon, ozone, and others are dissolved in the solvent nitrogen gas. Another example is found in "gold" jewelry. Most of the golden jewelry sold in the world is not 24 karat (i.e. 100% pure gold) but rather it is a solution of other metals, commonly silver and copper, in a gold solvent. Such a solution of metal(s) in another metal is called an amalgam.
Perhaps the most important property of a solution is its concentration. A dilute acetic acid solution, also called vinegar, is used in cooking while a concentrated solution of acetic acid would kill you if ingested. The only difference between such solutions is the concentration of the solute. In order to quantify the concentrations of solutions, chemists have devised many different units of concentration each of which is useful for different purposes.
Molarity, the number of moles of solute per liter of solution, has the units moles / L which are abbreviated M. This unit is the most commonly used measure of concentration. It is useful when you would like to know the number of moles of solute when you know both the molarity and the volume of a solution. For example, it is easy to calculate the volume of a 1.5 M solution of HCl necessary to completely react with 0.32 moles of NaOH:
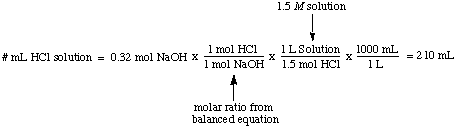
Normality, the number of molar equivalents of solute per liter of solution, has the units equivalents / L which are abbreviated N. To illustrate the difference between molarity and normality let's assume that we had used a 1.5 M solution of sulfuric acid, H2SO4, instead of a 1.5 M solution of hydrochloric acid, HCl in the above example. Because sulfuric acid can donate two protons to the NaOH, as noted in the , it will only take half as much sulfuric acid as hydrochloric acid to neutralize the sodium hydroxide.

In the present example, the 1.5 M solution of sulfuric acid reacts like a 3.0 M solution of hydrochloric acid because there are two equivalents of H+ per mole of sulfuric acid. Therefore, that solution of sulfuric acid is 3.0 N.
Please wait while we process your payment





