Enthalpy
Enthalpy is defined as how much heat a substance has at a given temperature
and pressure, and is symbolized by the symbol H. This temperature and
pressure is usually
STP. Although
there is no way to measure the absolute enthalpy of a substance, changes in
enthalpy can be measured.
Heat of Reaction
The change in enthalpy for a reaction is known as the heat of reaction and
has symbol δH. δH is negative for all exothermic reactions and
positive for all endothermic reactions.
The states (gas, liquid, solid) of all products and reactants must be stated in
any reaction involving enthalpy. Note how the state of the product in the
following two reactions affects δH.
| | | H2 +1/2O2→H2O (gas) δH = - 241.8 kJ |
|
| | | H2 +1/2O2→H2O (liquid) δH = - 285.8 kJ |
|
Heat of Formation
The heat of formation is defines as the δH
The next term you need to be familiar with is the standard heat of
formation. It is defined as the δH for a reaction that produces 1
mole of compound from its constituent elements. It has its own special symbol,
δHf. When solving enthalpy problems, you can find the heat of reaction
using the following formula:
| δH = δHf (products) - δHf (reactants) |
|
Sample Problems
Problem: Find δH for the reaction of sulfur dioxide with oxygen to form
sulfur trioxide given the following heats of formation:
| | | δHfSO2 = - 296.8 kJ / mole |
|
| | | δHfSO3 = - 395.7 kJ / mole |
|
Solution: First write a balanced equation:
In this case, no conversion of moles or mole ratio is necessary. Based on the
coefficients, simply assume 2 moles
2SO2(g) and 1 mole
O2(g). You want to find
δH for the basic equation not a special case.
You probably noticed that the
δHf for
O2
was not given. It is important to realize that the heat of formation for any
element in its basic state is arbitrarily set to 0 kJ / mole. The diatomic
molecules
H2(g),
N2(g),
O2(g),
F2(g),
Cl2(g),
Br2(l), and
I2(s) are
included in the grouping of elements in their fundamental states. Knowing this,
let's find the components needed for the
δH equation.
| | | δH (reactants) = 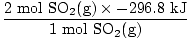 + + 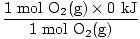 = - 593.6 kJ = - 593.6 kJ |
|
| | | δHf products = 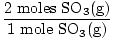 = - 791.4 kJ = - 791.4 kJ |
|
Now solve.
| δH = δHF (products) - δHF (reactants) = - 791.4 kJ - (- 593.6 kJ) = - 197.8 kJ |
|