Simplifying Square Roots (Review)
Let's review the steps involved in simplifying square roots:
- Factor the number inside
the square
root sign.
- If a factor appears twice, cross out both and write the factor
one time to the
left of the square root sign. If the factor appears three times, cross
out two of the factors
and write the factor outside the sign, and leave the third factor
inside the sign.
Note: If a factor appears 4, 6, 8, etc. times, this counts as 2, 3,
and 4 pairs, respectively.
- Multiply the numbers outside the sign. Multiply the numbers left
inside the
sign.
- Check: The outside number squared times the inside number should
equal the original number inside the square root.
To simplify the square root of a fraction, simplify the numerator and
simplify the
denominator.
Example 1: Simplify 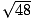
-
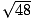 =
= 
-
 = 2×2
= 2×2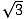
-
2×2
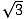 = 4
= 4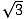
- Check: 42(3) = 48
Thus,
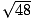 = 4
= 4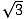
.
Example 2: Simplify
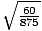
.
First, reduce the fraction to lowest terms:
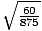 =
= 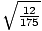
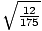 =
= 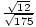
Numerator:
-
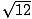 =
= 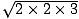
-
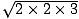 = 2
= 2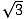
-
2
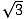 = 2
= 2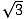
- Check: 22(3) = 12
Denominator:
-
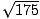 =
= 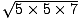
-
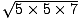 = 5
= 5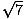
-
5
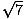 = 5
= 5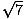
- Check: 52(7) = 175
Thus,
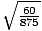 =
= 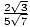 .
.
Rationalizing the Denominator
In addition to simplifying the numerator and the denominator in a fraction, it is
mathematical convention to rationalize the denominator--that is, to write the
fraction as an equivalent expression with no roots in the denominator.
To rationalize a denominator, multiply the fraction by a "clever" form
of 1--that is, by a fraction whose numerator and denominator are
both equal to the square root in the denominator. For example, to
rationalize the denominator of 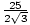 , multiply the
fraction by
, multiply the
fraction by  :
:
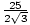 ×
× =
=  =
= 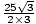 =
= 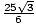 .
.
Thus, 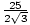 =
= 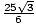 .
.
Often, the fraction can be reduced:
Rationalize the denominator of 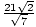 :
:
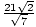 ×
×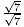 =
= 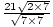 =
= 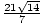 =
=  = 3
= 3 .
.
Thus, 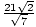 = 3
= 3 .
.