Review of Terminology
- An expression is a "phrase" that represents a number.
- An equation sets two expressions equal to each other.
A variable is a symbol used to represent a number. In the expression 8x + 17, x is the variable. In the equation 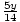 = 25, y is the variable. Variables need not be letters; for example, the expression 6
= 25, y is the variable. Variables need not be letters; for example, the expression 6 + 2 contains the variable
+ 2 contains the variable  .
.
An expression or equation may contain more than one variable. The expression 7 - 3r + 12t contains the variables r and t, and the equation 6y = 24x contains the variables x and y.
An algebraic expression is an expression that contains one or more variables.
An algebraic equation is an equation that contains one or more variables.
Note: When we write two quantities next to each other, or next to each other separated by parenthesis, the multiplication sign is implied. For example, 4r means 4×r and 3(4 + 2) means 3×(4 + 2).
Translating Word Statements into Algebraic Expressions and Equations
We can represent word statements by algebraic expressions and equations. For example, "the number of apples in the bucket plus 5 more apples" can be represented by the expression a + 5. The statement "twice the number of miles I ran is equal to 12" can be represented by the equation 2m = 12. Here are the steps to writing a word statement as an expression or an equation:
- Identify the unknown quantity (or quantities).
- Choose variable(s) to represent the unknown(s).
- Identify the operations on the variables.
If a phrase asserts that two quantities are equal, then it is mathematically expressed by an equation. To determine this equation's component expressions, separate the two quantities and follow the above steps for each.