Expressions and Equations

Solving Equations Using Inverse Operations

Reversing Operations

The goal in solving an equation is to get the variable by itself on one side of the equation and a number on the other side of the equation.

To isolate the variable, we must reverse the operations acting on the variable. We do this by performing the inverse of each operation on both sides of the equation. Performing the same operation on both sides of an equation does not change the validity of the equation, or the value of the variable that satisfies it.

Reversing Multiple Operations

When more than one operation acts on a variable in an algebraic equation, apply the reverse of the order of operations to reverse the operations. Here is the order in which you should reverse operations:

1. Reverse addition and subtraction (by subtracting and adding) outside parentheses.
2. Reverse multiplication and division (by dividing and multiplying) outside parentheses.
3. Remove (outermost) parentheses, and reverse the operations in order according to these three steps.

Be sure to check your answer! The value of the variable, when plugged in for the variable, should make the equation true.

Example 1: Solve for x : 5x + 9 = 44

1. Reverse addition: 5x + 9 - 9 = 44 - 9
   5x = 35
2. Reverse multiplication: =
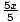   x = 7
3. No parentheses.

Check: 5(7) + 9 = 44

Thus, x = 7 .

Example 2: Solve for y : 3(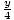 - 1) = 15

1. No addition or subtraction outside the parentheses
2. Reverse multiplication: 3( 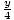-1)÷3 = 15÷3
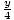   ( - 1) = 5
3. Within parentheses:
   1. Reverse subtraction: 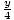- 1 + 1 = 5 + 1
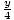      = 6
   2. Reverse division: 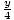×4 = 6×4
      y = 24
   3. No parentheses.

Check: 3(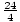 - 1) = 15
Thus, y = 24 .

Example 3: Solve for z : 4(3(z - 11) + 6) = 48

1. No addition or subtraction.
2. Reverse multiplication: =
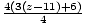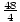
   (3(z - 11) + 6) = 12
3. Within parentheses:
   1. Reverse addition: 3(z - 11) + 6 - 6 = 12 - 6
      3(z - 11) = 6
   2. Reverse multiplication: =
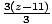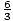
      (z - 11) = 2
   3. Within parentheses
      1. Reverse subtraction: z - 11 + 11 = 2 + 11
         z = 13
      2. No multiplication or division.
      3. No parentheses.

Check: 4(3(13 - 11) + 6) = 48
Thus, z = 13 .

Sometimes, the equation will not start out simplified. If this is the case, simplify the equation before reversing the operations.

Example 4: Solve for x : 6x - 5 - 2x + 3 - 2 = 4

First, simplify the equation by combining like terms: 4x - 4 = 4

1. Reverse subtraction: 4x - 4 + 4 = 4 + 4
   4x = 8
2. Reverse multiplication: =
   x = 2
3. No parentheses.

Check: 6(2) + 5 - 2(2) - 3 + 2 = 12 - 5 - 4 + 3 - 2 = 4

Thus, x = 2