We can solve inequalities using inverse operations in the same way we solve
equations using inverse operations with one exception: we have to pay attention to
the rules governing multiplication and division by a negative number and reciprocals, and
flip the inequality sign when appropriate.
Again, follow these steps to reverse the order of operations acting on the variable:
- Reverse addition and subtraction (by subtracting and adding)
outside parentheses.
- Reverse multiplication and division (by dividing and multiplying)
outside parentheses. When multiplying or dividing by a negative
number, flip the inequality sign. It does not matter if the number
being divided is positive or negative.
- Remove (outermost) parentheses, and reverse the operations in order
according to these three steps.
The answer should be an inequality; for example,
x < 5.
To solve an inequality with a "≠" sign, change the "≠" sign
into an "=" sign, and solve the equation. Then, change the "="
sign in the answer to a "≠" sign. This works because determining
the values of x for which two expressions are not equal is
the same as determining the values for which they are equal and
excluding them from the replacement set.
Example 1: 5x - 8 < 12
5x - 8 + 8 < 12 + 8
5x < 20
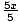 <
< 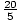
x < 4
Example 2: 4 - 2x≤2x - 4
4 - 2x + 2x≤2x - 4 + 2x
4≤4x - 4
4 + 4≤4x - 4 + 4
8≤4x
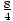 ≤4x4
≤4x4
2≤x
x≥2
Example 3: 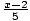 ≥ - 6
≥ - 6
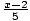 ×5≥ -6×5
×5≥ -6×5
The number being divided is negative, but the number we are dividing by is
positive, so the sign does not flip.
x - 2≥ - 30
x - 2 + 2≥ - 30 + 2
x≥ - 28
Example 4: -3(x + 2) > 9
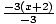 <
<
x + 2 < - 3
x + 2 - 2 < - 3 - 2
x < - 5
Example 5: 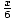 +2≠
+2≠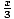 - 5
- 5
Solve 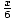 +2 =
+2 = 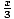 - 5
- 5
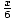 +2 -
+2 - 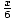 =
= 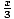 -5 -
-5 - 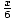
2 = 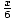 - 5
- 5
2 + 5 = 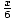 - 5 + 5
- 5 + 5
7 = 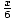
7×6 = 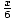 ×6
×6
42 = x
x = 42
Thus, the solution to our original inequality is x≠42.