Previous Next

Inverse Variation

The statement "y varies inversely as x means that when x increases, ydecreases by the same factor. In other words, the expression xy is constant:

xy = k    

where k is the constant of variation.
We can also express the relationship between x and y as:

y =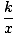    

where k is the constant of variation.

Since k is constant, we can find k given any point by multiplying the x-coordinate by the y-coordinate. For example, if y varies inversely as x, and x = 5 when y = 2, then the constant of variation is k = xy = 5(2) = 10. Thus, the equation describing this inverse variation is xy = 10 or y = .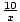

Example 1: If y varies inversely as x, and y = 6 when x = 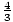, write an equation describing this inverse variation.

k = 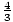(6) = 8
xy = 8 or y =

Example 2: If y varies inversely as x, and the constant of variation is k = 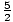, what is y when x = 10?

xy =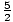
10y =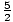
y = × = × =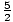

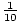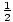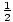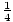
k is constant. Thus, given any two points (x1, y1) and (x2, y2) which satisfy the inverse variation, x1y1 = k and x2y2 = k. Consequently, x1y1 = x2y2 for any two points that satisfy the inverse variation.

Example 3: If y varies inversely as x, and y = 10 when x = 6, then what is y when x = 15?

x1y1 = x2y2
6(10) = 15y
60 = 15y
y = 4
Thus, when x = 6, y = 4.

Previous section Next page Inverse Variation page 2

Take a Study Break