Algebra II: Factoring

Factoring Polynomials of Degree 3

Factoring a ³ - b ³

An expression of the form a ³ - b ³ is called a difference of cubes. The factored form of a ³ - b ³ is (a - b)(a ² + ab + b ²) :

(a - b)(a ² + ab + b ²) = a ³ - a ² b + a ² b - ab ² + ab ² - b ³ = a ³ - b ³

For example, the factored form of 27x ³ - 8 ( a = 3x, b = 2 ) is (3x - 2)(9x ² + 6x + 4) .

Similarly, the factored form of 125x ³ -27y ³ ( a = 5x, b = 3y ) is (5x - 3y)(25x ² +15xy + 9y ²) .

To factor a difference of cubes, find a and b and plug them into (a - b)(a ² + ab + b ²) .

Factoring a ³ + b ³

An expression of the form a ³ + b ³ is called a sum of cubes. The factored form of a ³ + b ³ is (a + b)(a ² - ab + b ²) :

(a + b)(a ² - ab + b ²) = a ³ + a ² b - a ² b - ab ² + ab ² + b ³ = a ³ - b ³ .

For example, the factored form of 64x ³ + 125 ( a = 4x, b = 5 ) is (4x + 5)(16x ² - 20x + 25) .

Similarly, the factored form of 343x ³ + y ³ ( a = 7x, b = y ) is (7x + y)(49x ² -7xy + y ²) .

To factor a sum of cubes, find a and b and plug them into (a + b)(a ² - ab + b ²) .

You can remember these two factored forms by remembering that the sign in the binomial is always the same as the sign in the original expression, the first sign in the trinomial is the opposite of the sign in the original expression, and the second sign in the trinomial is always a plus sign.

Factoring ax ³ + bx ² + cx + d

ax ³ + bx ² + cx + d can be easily factored if 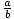= 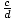First, group the terms: (ax ³ + bx ²) + (cx + d ) . Next, factor x ² out of the first group of terms: x ²(ax + b) + (cx + d ) . Factor the constants out of both groups. This should leave an expression of the form d ₁ x ²(ex + f )+ d ₂(ex + f ) . We can add these two terms by adding their "coefficients": (d ₁ x ² + d ₂)(ex + f ) .

Example 1: Factor 3x ³ +6x ² + 4x + 8 .

3x ³ +6x ² -4x - 8 = (3x ³ +6x ²) + (4x + 8) = 3x ²(x + 2) + 4(x + 2) = (3x ² + 4)(x + 2) .

Example 2: Factor 45x ³ +18x ² - 5x - 2 .

45x ³ +18x ² -5x - 2 = (45x ³ +18x ²) - (5x + 2) = 9x ²(5x + 2) - 1(5x + 2) = (9x ² - 1)(5x + 2) .
This can be further factored as a difference of squares: (9x ² - 1)(5x + 2) = (3x + 1)(3x - 1)(5x + 2) .