Adding or Subtracting Rational Expressions with Like Denominators
To add or subtract rational expressions with like denominators, add
or subtract their numerators and write the result over the denominator.
Then, simplify and factor the numerator, and write the expression in
lowest terms.
This is similar to adding two
fractions with like denominators, as in.
Example 1: 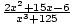 +
+ 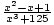 =?
=?
= 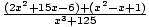
= 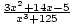
= 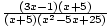
= 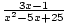 .
.
Example 2: 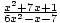 -
- 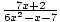 =?
=?
= 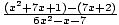
= 
= 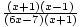
= 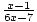 .
.
Adding or Subtracting Rational Expressions with Unlike Denominators
In Pre-Algebra, we learned that
fractions can be added or subtracted if and only if they have the same
denominator. Similarly, rational expressions can be added or subtracted
if and only if they have the same denominator. Thus, to add or subtract
two rational expressions with unlike denominators, we must
rewrite them as expressions with a common denominator.
PARAGARPH
To find the least common denominator of two
rational expressions, factor their denominators. The least common
denominator is the product of all the factors that appear in either
denominator--it is the union of the two sets
of factors (if a factor appears once in both denominators, only count it
once, but if a factor appears twice in one denominator, count it twice).
Leave the least common denominator in factored form.
Next, determine which factor(s) each denominator must be multiplied by
in order to yield the least common denominator--i.e. all the factors
in the LCD that do not appear in each denominator. Multiply each
fraction by this factor in the numerator and denominator, so as
not to change the fraction. Simplify the numerators and add (or
subtract) the two "converted" fractions with like denominators.
Simplify and factor the numerator, and write the resulting fraction in
lowest terms.