Rational Expressions

Solving Rational Equations

Solving Rational Equations

To solve a rational equation, such as 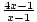+1 - 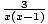= 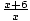, rewrite all the terms of the equation as fractions with a common denominator. For example, 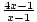+1 - 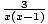= 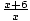can be rewritten as:

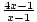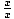× +1× - × = ×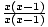

+ - =

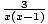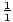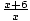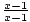
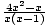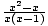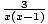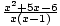
Next, eliminate the denominator:
4x ² - x + x ² - x - 3 = x ² + 5x - 6

Solve the equation:

5x ² -2x - 3 = x ² + 5x - 6
4x ² - 7x + 3 = 0
(4x - 3)(x - 1) = 0
x = 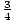, 1


Since we cannot divide by zero, we must check to see if any of the x -values yield 0 in the denominator. If an x -value produces 0 in the denominator, it is not a solution. x = 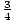does not produce 0 in any of the denominators, but x = 1 does produce 0 in one of the denominators. Thus, x = 1 is not a solution. The solution set is .

Remember to check all your solutions. If a number yields zero in any of the denominators, it is not a solution.