Trigonometric derivatives
The basic trigonometric functions have derivatives that should be memorized:
If x is expressed in radians, then:
| (sin(x))' | | = cos(x) |
|
| (cos(x))' | | = - sin(x) |
|
| (tan(x))' | | = sec2(x) = 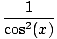 |
|
The Chain Rule
This is a rule for evaluating the derivatives of composite
functions
 fog fog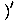 | | =  f'(g(x) f'(g(x)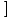 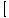 g'(x) g'(x)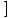 |
|
| | | or |
|
| (f (g(x))' | | = 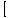 f'(g(x) f'(g(x)  g'(x) g'(x) |
|
For example, the function f (x) = (3x + 2)2 is a composite function where the outer
function, f, is a power function (u2), and the inner function, g, is a linear
function (3x + 2).
To differentiate this composite function, first treat the inner function as a single variable, and
take the derivative of the outer function. Then multiply by the derivative of the inner
function:
Implicit Differentiation
This is a means of finding 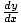 , the derivative of y with respect to x,
even when we do not have a function of the form y = f (x).
, the derivative of y with respect to x,
even when we do not have a function of the form y = f (x).
Example: Find the slope of the graph at (0, 0) for the following function:
To solve this problem, we must essentially first find 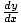 and then plug in the
point (0,0) to find the slope.
and then plug in the
point (0,0) to find the slope.