Differentiable  -  A function f is said to be differentiable at a point x = a if f'(a) exists.

Difference Quotient  -  The difference quotient,

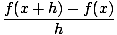
represents the slope of an arbitrary secant line connecting the point (x, f (x)) and the nearby point (x + h, f (x + h)) on the graph of f.

Derivative  -  The derivative of f is denoted as f'(x), and it is the function that gives the slope of the graph of f at the point (x, f (x)). Written as the limit of the difference quotient, the derivative of f (x) is

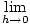
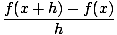
Secant  -  The secant line is a line connecting two points on the same curve

Tangent  -  The tangent to a curve is the line that just touches the curve at one point. At the point where the tangent meets the curve, they have the same slope.