In this section, we introduce the basic techniques of differentiation and apply them to
functions built up from the elementary functions.
Basic Properties of Differentiation
There are two simple properties of differentiation that make the calculation of derivatives
much easier. Let f (x), g(x) be two functions, and let c be a constant. Then
-
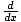 [cf (x)] = cf'(x)
[cf (x)] = cf'(x)
-
(f + g)'(x) = f'(x) + g'(x)
In words, these properties say that the derivative of a constant times a function is that
constant times the derivative of the function, and the derivative of a sum of functions is
the sum of the derivatives of the functions.
Product Rule
Given two functions f (x), g(x), and their derivatives f'(x), g'(x), we would like
to be able to calculate the derivative of the product function f (x)g(x). We do this by follwowing the
product rule:
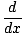 [f (x)g(x)] [f (x)g(x)] | = | 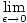 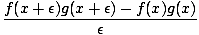 |
|
| | = | 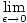 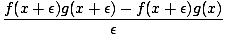 + + 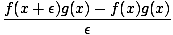 |
|
| | = | 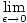 f (x + ε) f (x + ε)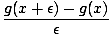 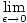 g(x) g(x)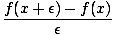 |
|
| | = | f (x)g'(x) + g(x)f'(x) |
|
Quotient Rule
Now we show how to express the derivative of the quotient of two functions f (x),
g(x) in terms of their derivatives f'(x), g'(x). Let q(x) = f (x)/g(x). Then
f (x) = q(x)g(x), so by the product rule, f'(x) = q(x)g'(x) + g(x)q'(x). Solving for
q'(x), we obtain
This is known as the quotient rule. As an example of the use of the quotient rule, consider the rational function
q(x) = x/(x + 1). Here f (x) = x and g(x) = x + 1, so
Chain Rule
Suppose a function h is a composition of two other functions, that is, h(x) = f (g(x)).
We would like to express the derivative of h in terms of the derivatives of f and g.
To do so, follow the chain rule, given below: