For the infinite boomerang, we obtain:
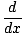 [x2y2] [x2y2] | = | 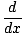 [x + y] [x + y] |
|
| x2(2yy') + y2(2x) | = | 1 + y' |
|
| y'(2x2y - 1) | = | 1 - 2xy2 |
|
| y' | = | 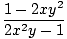 |
|
Therefore, at the point (0, 0), the slope of the graph is -1. Note that we
cannot just plug any point we like into this formula--the point must be a solution
to the original equation in order for the answer to make sense.
Differentiation of Inverse Functions
We can put the chain rule and implicit differentiation to work to find the
derivative of an inverse function when we already know the derivative of the
function itself. Suppose we are given a function f (x) with derivative f'(x) and
let g(x) be its inverse, so that g(f (x)) = f (g(x)) = x. Differentiating both sides
of f (g(x)) = x, we obtain:
| f'(g(x))g'(x) | = | 1 |
|
| g'(x) | = | 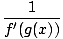 |
|
Let us use this technique to find the derivative of the inverse sine function,
f (x) = sin-1(x), defined on the interval [- 1, 1] and taking values in [- Π/2, Π/2].
Since f'(x) = cos(x), the formula tells us that
g'(x) = 1/cos(sin-1(x)) = 1/ . The derivatives of the other inverse
trigonometric functions are as follows:
. The derivatives of the other inverse
trigonometric functions are as follows: