In this section we present the fundamental theorem of calculus. First, we must make
a definition. A function F(x) is called an antiderivative of a function f (x) if
f (x) is the derivative of F(x); that is, if F'(x) = f (x). The antiderivative of
a function f (x) is not unique, since adding a constant to a function does not change
the value of its derivative:
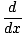 (f (x) + c) = (f (x) + c) = 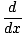 (f (x)) + (f (x)) + 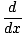 (c) = (c) = 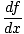 |
|
It is true, however, that any two antiderivatives of a function f (x) will differ by a
constant.
Why are antiderivatives a useful concept? Because they provide a shortcut for
calculating definite integrals, as shown by the first part of the fundamental theorem of
calculus.
Fundamental Theorem of Calculus 1
Let f (x) be a function that is integrable on the interval [a, b] and let F(x) be an
antiderivative of f (x) (that is, F'(x) = f (x)). Then
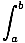 f (x)dx = F(b) - F(a) f (x)dx = F(b) - F(a) |
|
Since the expression F(b) - F(a) is one we will encounter often, we will sometimes
employ a special shorthand to simplify our equations:
Note that any antiderivative F(x) will give the same value for F(b) - F(a), since any
two antiderivatives differ only by a constant, which will cancel upon subtraction. The
formula in the theorem may also be written