All of the elementary functions are continuous (because they are continuous at the
x-values where they are defined.
Sometimes we want to talk about the limit of a function as x approaches infinity or
negative infinity (∞ or - ∞). This is essentially the same idea: approaching
∞ means that x is getting larger and larger; approaching - ∞ means smaller
and smaller.
Rigorous Definitions
We now make precise the intuitive definitions of limit and continuity given above. Let
f be a function from some subset of the real numbers to the real numbers and let x0
be a real number. Then the function f is said to have limit L at x0 if for all
ε > 0, there exists a δ > 0 such that 0 < | x - x0| < δ implies | f (x) - L| < ε. If this is the case, we write
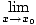 f (x) = L f (x) = L |
|
As above, if a function f has a limit L = f (x0) at x0, then f is said to be
continuous at x0. A function that is continuous at every point in its domain is said to
be a continous function.
As an example of a proof that uses this definition, we show that the linear function
f (x) = 3x is continuous at x0 = 1. Given ε > 0, we choose δ = ε/3.
Suppose | x - 1| < δ. Then | f (x) - f (1)| = | 3x - 3| = 3| x - 1| < 3δ = ε. Therefore the
limit of f (x) at x = 1 is f (1) = 3, and f is continuous there.
Intermediate Value Theorem
We conclude by mentioning an important property of continuous functions. Suppose
f (x) is continuous on an interval [a, b]. Let y be any number between f (a) and
f (b). Then the intermediate value theorem states that there exists c in the
interval (a, b) such that f (c) = y.