This final application, that of finding the distance traveled by an object given its velocity
at each moment, follows directly from the fundamental theorem of calculus. Suppose an
object is moving in a straight line, and let its velocity at time t be given by the function
f (t). We saw earlier on, while working with derivatives, that the function F(t) giving
the position of the object at time t is an antiderivative of the velocity function f (t):
Let us suppose that we know the velocity function f (t) (and the initial position of the
object at t = 0) and want to determine the position function F(t). To compute the
distance the object travels from time 0 to time b, F(b) - F(0), we apply the
Fundamental Theorem of Calculus:
F(b) - F(a) = 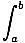 f (x)dx f (x)dx |
|
So the area under the graph of a velocity function gives the distance traveled.