The natural rules for the definite integral of sums and constant
multiplies of functions, i.e.
sumrule, constmult
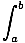 (f (x) + g(x))dx (f (x) + g(x))dx | | = 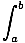 f (x)dx + f (x)dx + 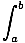 g(x)dx g(x)dx |
|
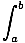 cf (x)dx cf (x)dx | | = c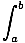 f (x)dx f (x)dx |
|
follow (by the Fundamental Theorem of Calculus) from the similar rules
for antiderivatives, as we know prove.
Let F(x) and G(x) be two functions with F'(x) = f (x), G'(x) = g(x). We know by the
addition rule for derivatives that
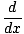 F(x) + F(x) + 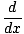 G(x) = G(x) = 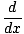 [F(x) + G(x)] [F(x) + G(x)] |
|
Writing this in terms of f and g yields
f (x) + g(x) = 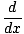 [ [ f (x)dx + f (x)dx +  g(x)dx] g(x)dx] |
|
As functions of b, the left and right hand sides of @@the sum
rule@@ are antiderivatives of the two expressions above, so
they differ by a constant. This constant must be zero, however, since
the integrals are equal (both zero) for b = a, and the sum rule is
proved.
Similarly, if c is a constant, we know that
c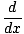 F(x) = F(x) = 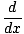 [cF(x)] [cF(x)] |
|
or
cf (x) = 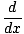 [c [c f (x)dx] f (x)dx] |
|
As before, the @@constant multiple rule@@ asserts the
equality of antiderivatives of these two expressions that agree for
one value of b. Therefore the antiderivatives are equal, and the
rule follows.