The integration by parts method comes from the product
rule for derivatives. Given two functions f, g, the
product rule states that
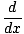 [f (x)g(x)] = f'(x)g(x) + f (x)g'(x) [f (x)g(x)] = f'(x)g(x) + f (x)g'(x) |
|
As usual, equating antiderivatives of these two expressions that agree at one point, we obtain
a formula for definite integrals:
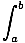 f (x)g'(x)dx = f (x)g(x)|ab - f (x)g'(x)dx = f (x)g(x)|ab - 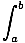 f'(x)g(x)dx f'(x)g(x)dx |
|
This final formula is integration by parts. It is useful when the function we want to
integrate is the product of one function (f) for which we know the derivative and another
function (g') for which we know the antiderivative.