Previous Next

Problem : Consider the parametric curve (x(t), y(t)) = (2t, sin(t)). What function has a graph that coincides with this curve?

Substituting t = x(t)/2 in the expression for y(t) yields y(t) = sin(x(t)/2). Thus the desired function is f (x) = sin(x/2).

Problem : What is the velocity vector of the parametric curve (2t, sin(t)) at time t = 0? Π/2? Π?

The derivatives of the parametric functions are x'(t) = 2, y'(t) = cos(t), so the velocity vectors given by


(x'(0), y'(0))=(2, 1)  
(x'(Π/2), y'(Π/2))=(2, 0)  
(x'(Π), y'(Π))=(2, - 1)  

Problem : What is the velocity vector at time t = 2Πk (k≥ 0 an integer) of the spiral (t cos(t), t sin(t))? Suppose a particle is tracing out the spiral, so that it is at the point (t cos(t), t sin(t)) at time t. How fast is the particle moving at time t?

Since (x'(t), y'(t)) = (cos(t) - t sin(t), sin(t) + t cos(t)), the desired velocity vectors are given by

(x'(2Πk), y'(2Πk)) = (1, 2Πk)    

The speed of the particle at time t is equal to

=    

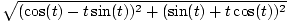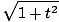This makes sense because the speed of the particle must continue to rise if it is to continue to complete larger and larger turns of the spiral in the same amount of time (2Π).
Previous section Next section

Take a Study Break