Problem :
Determine if the series
converges.
If
an is the
n-th term of the series, then
For large
n, this quotient is very close to
1/2. Hence, for all
but the first few integers
n, the quotient will be
≤3/4.
Since we may disregard the first few terms when considering questions
of convergence, the ratio test implies that the series converges.
Problem :
Suppose x is a fixed real number. Determine whether or not the series
converges.
Letting
an equal the
nth term of the series, we have
Since this ratio is clearly less than, say,
1/2 for all but the
first few
n, the ratio test implies that it converges.
Problem :
Show that the series
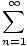 1/rn 1/rn |
|
converges for any real number
r > 1.
If
an is the
nth term of the series, then
Since
1/r < 1 whenever
r > 1, the ratio test implies that the
series converges.