Problem :
Use the integral test to show that 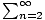 1/(n(log(n))2) converges.
1/(n(log(n))2) converges.
Letting
u = log(x), we compute the relevant integral:
The limit of this integral as
m→∞ exists and is equal to
1/log(2), so the
sum converges by the integral test.
Problem :
Show that the series
diverges using the integral test.
Letting
u = x3 + 1, we compute the relevant integral:
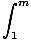 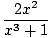 dx dx | = | 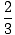 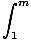 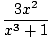 |
|
| | = | 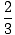 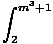  du du |
|
| | = | 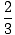 (log(u)|2m3+1) (log(u)|2m3+1) |
|
| | = | 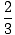 log log 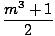 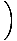 |
|
This quantity clearly has no limit as
m→∞, so the series
diverges. Notice that there are far more efficient ways to show the divergence
of this series; for instance one could use the comparison test with the
harmonic series
1/n.