Until the final section of this chapter, we will restrict our attention to series with an≥ 0. Thus the partial sums are increasing:
If the series  an is to converge, there must be some B such that
sn≤B for all n, or the sn will become arbitrarily large. Such a B is called
an upper bound. The value to which the series converges is the least of all possible
upper bounds. It turns out that whenever the sequence {sn} of partial sums has an
upper bound, there exists a least upper bound, to which the series converges. This fact
enables us to prove the comparison test, stated below.
an is to converge, there must be some B such that
sn≤B for all n, or the sn will become arbitrarily large. Such a B is called
an upper bound. The value to which the series converges is the least of all possible
upper bounds. It turns out that whenever the sequence {sn} of partial sums has an
upper bound, there exists a least upper bound, to which the series converges. This fact
enables us to prove the comparison test, stated below.
For two series  an,
an,  bn, with an, bn≥ 0 for all n, suppose there exists a number C > 0 such that
bn, with an, bn≥ 0 for all n, suppose there exists a number C > 0 such that
for all n and that  bn converges. Then
bn converges. Then  an
converges and
an
converges and
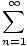 an≤C an≤C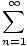 bn bn |
|
To prove this statement, it suffices to show that the number C bn is
a bound for the partial sums a1 + a2 + ... + an. Then the least upper bound of these
partial sums must exist and is clearly less than or equal to C
bn is
a bound for the partial sums a1 + a2 + ... + an. Then the least upper bound of these
partial sums must exist and is clearly less than or equal to C bn.
Thus we need only note that
bn.
Thus we need only note that
| a1 + ... + an | ≤ | Cb1 + ... + Cbn |
|
| | = | C(b1 + ... + bn) |
|
| | ≤ | C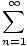 bn bn |
|
A similar test enables us to show that certain series diverge. If  an
and
an
and  bn are again two series with an, bn≥ 0 for all n,
suppose that there exists C≥ 0 such that an≥Cbn for all n and that
bn are again two series with an, bn≥ 0 for all n,
suppose that there exists C≥ 0 such that an≥Cbn for all n and that
 bn diverges. Then
bn diverges. Then  an also diverges. The
proof of this fact is similar to the previous proof--since the partial sums of the bn
become arbitrarily large and
an also diverges. The
proof of this fact is similar to the previous proof--since the partial sums of the bn
become arbitrarily large and
| a1 + ... + an≥Cb1 + ... + Cbn = C(b1 + ... + bn) |
|
the partial sums of the an also become arbitrarily large.