A geometric series is a series of the form  arn (where we take a
and r to be positive). One learns in high school algebra that this series converges if and
only if 0 < r < 1. If
arn (where we take a
and r to be positive). One learns in high school algebra that this series converges if and
only if 0 < r < 1. If  arn does converge, we have
arn does converge, we have
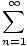 arn = arn = 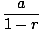 |
|
We can combine these comments about geometric series with the comparison test to yield
another test called the ratio test: given a series  an with an > 0 for all n, if
there exists a number C with 0 < C < 1 such that
an with an > 0 for all n, if
there exists a number C with 0 < C < 1 such that
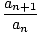 ≤C ≤C |
|
for all n, then  an converges.
an converges.
To prove this fact, note that under the hypotheses of the theorem,
| an≤Can-1≤C2an-2≤ ... ≤Cn-1a1 |
|
Letting bn = a1Cn-1, so that  bn is a (convergent)
geometric series, we see that an≤bn. By the comparison test,
bn is a (convergent)
geometric series, we see that an≤bn. By the comparison test,  an must also converge; in fact
an must also converge; in fact