We now investigate the convergence of power series, of which the Taylor series we
will encounter in the next SparkNote are a special case. A power series is a series
of the form
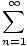 anxn anxn |
|
where the an are constants and x is a variable. In order to ask if a power series
converges, we must first specify the value of x. The n-th partial sum of such a series
looks like
a polynomial of degree n in the variable x.
One example of a power series is the series
where n! = n(n - 1)(n - 2) ... (2)(1). This series converges absolutely for all values of
x. To show this, we use the ratio test. Letting an = | x|n/n!, we have
Now | x|/(n + 1) < 1/2 for large enough n, so (disregarding as many initial terms of the
sequence as necessary) we see that the sequence converges.
We now state the key result concerning the convergence of power series. For each power
series  anxn, there exists a radius of convergence, r, which may
be either a nonnegative number or infinity. If r is a number, then
anxn, there exists a radius of convergence, r, which may
be either a nonnegative number or infinity. If r is a number, then  anxn converges absolutely whenever 0≤| x| < r and does not converge absolutely
whenever r < | x|. If r = ∞, then
anxn converges absolutely whenever 0≤| x| < r and does not converge absolutely
whenever r < | x|. If r = ∞, then  anxn converges absolutely
for all real numbers x.
anxn converges absolutely
for all real numbers x.
This fact allows us to define a function on the interval (- r, r) by setting
f (x) = 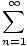 anxn anxn |
|
for all x with | x| < r. Let us return, by way of illustration, to the power series
 xn/n! introduced earlier. There is no reason why the index must
begin at 1. We may as well let it start at 0 (recalling that 0! = 1)--the radius of
convergence will still be ∞. The function thus defined for all real numbers,
xn/n! introduced earlier. There is no reason why the index must
begin at 1. We may as well let it start at 0 (recalling that 0! = 1)--the radius of
convergence will still be ∞. The function thus defined for all real numbers,
f (x) = 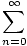 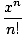 = 1 + x + = 1 + x + 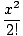 + + 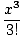 + ... + ... |
|
happens to be equal to the exponential function f (x) = ex. We will
return to this intriguing "coincidence" in the next chapter.