Previous Next

1 + x + + + ... =    

since e0 = 1. For any given x, the remainder term satisfies the inequality

| rn(x)| = ec = ec    

for some c between 0 and x. Since c≤x implies ec≤ex, a constant, and 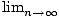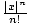= 0, we once again have that 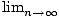| rn(x)| = 0, so the function defined by the Taylor series for f (x) = ex is equal to f (x) for all x.

The Logarithm Function

This time, since log(0) is not defined, we choose instead to find the Taylor series for f (x) = log(x) at x = 1. We compute the first few derivatives below:


f'(x) =  
f(2)(x) = -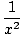  
f(3)(x) =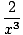  
f(2)(x) = -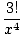  

Thus

f(n)(x) = (- 1)n-1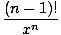    

for n≥1, so

f(n)(1) = (- 1)n-1(n - 1)!    

and the Taylor series for f (x) = log(x) at x = 1 is

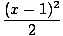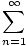(x - 1) - + - + ... = (- 1)n-1    

In this case, it turns out that the series only converges (to the value log(x)) for x in the interval (0, 2), i.e. the radius of convergence is 1. Letting y = x - 1, we may write

log(1 + y) = y - + - + ...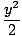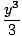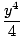    

for y in the interval (- 1, 1).

Previous page Some Common Taylor Series page 2 Next section

Take a Study Break