Polynomials are easy to differentiate and integrate, applying the respective sum
rules a finite number of times to reduce to the case of a monomial. We would
like to be able to do the same thing for power series
(including Taylor series in particular). It is a theorem that this always
works within the radius of convergence of the power series. We state the result
below.
Suppose f (x) = 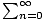 anxn is a power series with radius of convergence
r. Then for all x with | x| < r,
anxn is a power series with radius of convergence
r. Then for all x with | x| < r,
f'(x) = 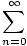 nanxn-1 nanxn-1 |
|
and
where C is an arbitrary constant, reflecting the non-uniqueness of the
antiderivative.