Terms
Taylor's Formula
-
A formula expressing a function in terms of a polynomial approximation and an error
(remainder) term. Explicitly, given a function
f (x) and a real number
a,
|
f (x) |
= |
f (a) + f'(a)(x - a) + ... + f(n-1)(a) +  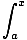f(n)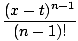(t) dt
|
|
| |
= |
pn-1(x) + rn(x) |
|
where
pn-1(x) is a Taylor polynomial and
rn(x) is the remainder term
Taylor Polynomial
-
The approximation of a function
f (x) around a point
x = a by a polynomial
pn(x) = f (a) + f'(a)(x - a) + 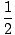 f''(a)(x - a)2 + ... +  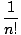f(n)(a)(x - a)n |
|
for some
n≥ 0.
Taylor Series
-
Given a function
f (x), the
Taylor series about
x = a is
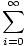
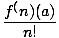  (x - a)n |
|
The Taylor polynomials for
f about
a are the partial sums of this series.
Remainder Term
-
The difference between a Taylor polynomial and a function it approximates.
