Problem :
Is the transverse axis of this hyperbola horizontal or vertical: - 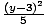 +
+ 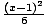 = 1.
= 1.
Because the
y2 term is negative, the transverse axis is horizontal.
Problem :
Find a, b, and c of the following hyperbola: 5x2 -3y2 - 20x + 6y + 2 = 0.
By completing the square, factoring, and putting the equation in standard
form, it is evident that
a = 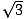
,
b = 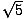
, and
c = 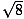
.
Problem :
The eccentricity of a hyperbola with center (0, 0) and focus 5, 0) is 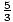 . What is the standard equation for the hyperbola?
. What is the standard equation for the hyperbola?
e = 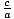
, so
c = 5,
a = 3, and
b = 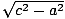 = 4
= 4. The
locations of the focus and the center mean that the transverse axis is
horizontal, and the
y2 term is negative. So the standard equation for this
hyperbola is
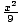 -
- 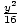 = 1
= 1.
Problem :
Find the asymptotes of the hyperbola
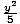 -
- 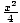 = 1.
= 1.
a = 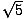
,
b = 2. The asymptotes are
y = 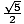 x
x and
y = - 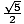 x
x.
Problem :
The transverse axis of a hyperbola is horizontal. One of the asymptotes is y = 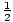 x + 5. What is the standard equation of the hyperbola?
x + 5. What is the standard equation of the hyperbola?
a = 1,
b = 2, and the center of the hyperbola is
(0, 5). The standard
equation, then, is
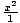 -
-  = 1
= 1.