Problem :
Is the following plane curve a function: y = 3t2, x = 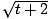 , 0≤t≤5?
, 0≤t≤5?
Yes. By examining the graph, you can see that for every
x, there is only one
f (x).
Problem :
The following plane curve is a circle: x = 2 cos(t), y = 2 sin(t), 0≤t < 2Π. Is its orientation clockwise or couterclockwise? What happens
when you reverse the parametric equations, so that x = 2 sin(t), y = 2 cos(t)?
The orientation of the first curve is counterclockwise. When the functions for
x and
y are exchanged, the curve's orientation becomes clockwise.
Problem :
Convert the parametric equation x = 2t, y = 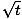 , t > 0, to a
rectangular equation.
, t > 0, to a
rectangular equation.
y = 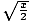
.
Problem :
How many times does the graph of x = t2 - t - 6, y = 2t, -5 < t < 5 cross
the y-axis?
Twice, when
t = - 2 at
(0, - 4) and when
t = 3 at
(0, 6).
Problem :
Jim and Bob are racing from the origin to the point (5, 10). Let t be the
number of seconds after the start of the race. Jim's position at any time t
is given by the parametric equations x = t, y = 2t. Bob's position at any
time t is given by the parametric equations x = 5t, y = 10t. Who will win
the race? How long does it take each competitor to finish the race?
Jim reaches the point
(5, 10) after
t = 5 seconds. Bob will reach the point
(5, 10) after
t = 1 second. Bob will win the race.